阅读理解:
材料1:对于一个关于x的二次三项式ax2+bx+c(a≠0),除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令ax2+bx+c=y(a≠0),然后移项可得:ax2+bx+(c-y)=0,再利用一元二次方程根的判别式来确定y的取值范围,请仔细阅读下面的例子:
例:求x2+2x+5的取值范围.
解:令x2+2x+5=y,∴x2+2x+(5-y)=0,∴Δ=4-4×(5-y)≥0,∴y≥4,∴x2+2x+5≥4.
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于x的一元二次方程ax2+bx+c=0(a>0)有两个不相等的实数根x1,x2(x1>x2),
则关于x的一元二次不等式ax2+bx+c≥0(a>0)的解集为:x≥x1或x≤x2.
则关于x的一元二次不等式ax2+bx+c≤0(a>0)的解集为:x2≤x≤x1.
请根据上述材料,解答下列问题:
(1)利用材料1,若关于x的二次三项式x2+ax+3(a为常数)的最小值为-6,求a的值;
(2)利用材料2,若关于x的代数式5mx-nx2-x+2(其中m、n为常数,且mn≠0)的最小值为-4,最大值为7,请求出满足条件的m,n的值.
5
mx
-
n
x
2
-
x
+
2
【答案】(1)a=6或a=-6;
(2)
或
.
(2)
m = 14 5 |
n = 7 4 |
m = - 14 5 |
n = - 49 4 |
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/17 13:0:8组卷:197引用:1难度:0.2
相似题
-
1.抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)解不等式-x2+(m-1)x+m>0.发布:2025/6/17 6:30:2组卷:6引用:1难度:0.5 -
 2.已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=1,则不等式ax2+bx+c>0的解集是.发布:2025/6/16 9:30:1组卷:894引用:10难度:0.9
2.已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=1,则不等式ax2+bx+c>0的解集是.发布:2025/6/16 9:30:1组卷:894引用:10难度:0.9 -
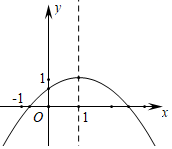 3.二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
3.二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx;⑤4ac<b2.
其中正确的有( )个发布:2025/6/16 22:30:4组卷:685引用:4难度:0.6


