我国著名数学家华罗庚先生说过：“数形结合百般好，隔裂分家万事休”，数形结合的思想方法在数学中应用极为广泛．
【规律探索】用同样大小的两种不同颜色的正方形纸片，按如图方式拼成长方形：
第（1）个图形中有2张正方形纸片；
第（2）个图形中有2（1+2）=2+4=6张正方形纸片；
第（3）个图形中有2（1+2+3）=2+4+6=12张正方形纸片；
第（4）个图形中有2（1+2+3+4）=2+4+6+8=20张正方形纸片；
…
请你观察上述图形与算式，完成下列问题：
【规律归纳】
（1）第（7）个图形中有5656张正方形纸片（直接写出结果）；
（2）根据上面的发现我们可以猜想：2+4+6+…+2n=n（n+1）n（n+1）（用含n的代数式表示）；
【规律应用】
根据你的发现计算：
①2+4+6+…+2000；
②202+204+206+…+600．
【答案】56；n（n+1）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/30 9:0:8组卷：804引用：3难度：0.5
相似题
-
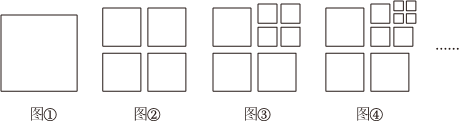
1．将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形……如此下去，则第2019个图中共有正方形的个数为（ ）
发布：2025/5/24 23:30:2组卷：327引用：3难度：0.7 -
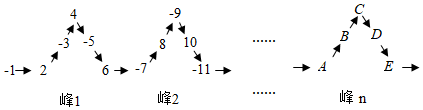
2．将一列有理数-1，2，-3，4，-5，6，…，如图所示有序排列．根据图中的排列规律可知，有理数4在“峰1”中C的处．则有理数-2021在（ ）
发布：2025/5/24 23:0:1组卷：274引用：3难度：0.6 -
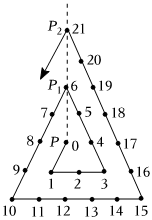3．如图所示，动点P从第一个数0的位置出发，每次跳动一个单位长度，第一次跳动一个单位长度到达数1的位置，第二次跳动一个单位长度到达数2的位置，第三次跳动一个单位长度到达数3的位置，第四次跳动一个单位长度到达数4的位置，……，依此规律跳动下去，点P从0跳动6次到达P1的位置，点P从0跳动21次到达P2的位置，…，点P1、P2、P3…Pn在一条直线上，则点P从0跳动（ ）次可到达P14的位置．发布：2025/5/25 0:0:2组卷：167引用：3难度：0.5
