根据以下素材，探索完成任务．
| 如何确定防守方案？ | ||||||||||||||||||
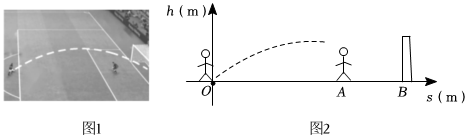
| 素材1 | 鹰眼系统能够追踪、记录和预测球的轨迹，如图分别为足球比赛中某一时刻的鹰眼系统预测画面（如图1）和截面示意图（如图2），足球的飞行轨迹可看成抛物线．攻球员位于O，守门员位于点A，OA的延长线与球门线交于点B，且点A，B均在足球轨迹正下方，已知OB=28m,AB=8m. |
|
||||||||||||||||
| 素材2 | 通过鹰眼系统监测，足球飞行的水平速度为15m/s.水平距离s（水平距离=水平速度×时间）与离地高度h的鹰眼数据如表．守门员的最大防守高度为 25 9 |
|
||||||||||||||||
| 问题解决 | ||||||||||||||||||
| 任务1 | 确定运动轨迹 | 求h关于s的函数表达式． | ||||||||||||||||
| 任务2 | 探究防守方案 | 若守门员选择原地接球，能否防守成功？若成功，请求出守门员接住球时，球的高度；若不成功，请通过计算说明理由． | ||||||||||||||||
| 任务3 | 拟定执行计划 | 求守门员选择面对足球后退，计算成功防守的最小速度． | ||||||||||||||||
【考点】二次函数的应用．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/25 14:0:1组卷：1670引用：3难度：0.2
相似题
-
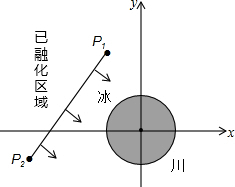1．为了考查冰川的熔化状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km的圆形考查区域，线段P1P2是冰川的部分边界线（不考虑其它边界），当冰川熔化时，边界线沿着与其垂直的方向朝考查区域平行移动，若经过n年，冰川的边界线P1P2移动的距离为s（km），并且s与n（n为正整数）的关系是s=n2-320n+950．以O为原点，建立如图所示的平面直角坐标系，其中P1、P2的坐标分别为（-4，9）、（-13、-3）．725
（1）求线段P1P2所在直线对应的函数关系式；
（2）求冰川边界线移动到考查区域所需的最短时间．发布：2025/6/18 19:30:1组卷：717引用：54难度：0.3 -
2．今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定：公共租赁住房和廉租住房并轨运行（以下简称并轨房），计划10年内解决低收入人群住房问题．已知第x年（x为正整数）投入使用的并轨房面积为y百万平方米，且y与x的函数关系式为y=-
x+5．由于物价上涨等因素的影响，每年单位面积租金也随之上调．假设每年的并轨房全部出租完，预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表：16
（1）求出z与x的函数关系式；时间x（单位：年，x为正整数） 1 2 3 4 5 … 单位面积租金z（单位：元/平方米） 50 52 54 56 58
（2）设第x年政府投入使用的并轨房收取的租金为W百万元，请问政府在第几年投入使用的并轨房收取的租金最多，最多为多少百万元？发布：2025/6/18 19:30:1组卷：424引用：51难度：0.1 -
3．在2014年巴西世界杯足球赛前夕，某体育用品店购进一批单价为40元的球服，如果按单价60元销售，那么一个月内可售出240套．根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高5元，销售量相应减少20套．设销售单价为x（x≥60）元，销售量为y套．
（1）求出y与x的函数关系式．
（2）当销售单价为多少元时，月销售额为14000元；
（3）当销售单价为多少元时，才能在一个月内获得最大利润？最大利润是多少？
[参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是]．（-b2a，4ac-b24a）发布：2025/6/18 19:30:1组卷：2230引用：58难度：0.1
