如图，在平面直角坐标系中，O为坐标原点，点B在x轴正半轴上，四边形OACB为平行四边形，OA=3m,cos∠AOB=33，反比例函数y=kx（k＞0）的图象在第一象限内过点A，且经过BC边的中点F，连接AF，OF．
（1）当m=10，即OA=103时，求反比例函数的表达式；
（2）设△OAF的面积为S，求S关于m的函数表达式；
（3）证明：△OAF∽△AFC
3
3
3
k
x
3
【考点】反比例函数综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/17 13:0:1组卷：759引用：2难度：0.3
相似题
-
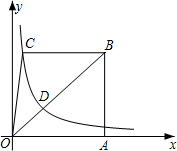1．如图，已知梯形ABCO的底边AO在x轴上，BC∥AO，AB⊥AO，过点C的双曲线交OB于D，且OD：DB=1：2，若△OBC的面积等于n,则k的值（ ）y=kx发布：2025/6/21 4:0:1组卷：287引用：3难度：0.9 -
2．定义：在平面直角坐标系中，过一点分别作坐标轴的垂线，若垂线与坐标轴围成矩形的周长的数值与面积的数值相等，则这个点叫做“和谐点”．
如图1，矩形ABOC的周长的数值与面积的数值相等，则点A是“和谐点”
（1）判断点E（2，3），F（4，4）是否为“和谐点”；
（2）如图2，若点P（a,b）是双曲线y=上的“和谐点”，求满足条件的所有P点坐标．18x
发布：2025/6/21 6:30:1组卷：538引用：46难度：0.5 -
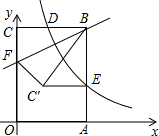3．以矩形OABC的顶点O为坐标原点建立平面直角坐标系，使点A、C分别在x、y轴的正半轴上，双曲线y=（x＞0）的图象经过BC的中点D，且与AB交于点E，过OC边上一点F，把△BCF沿直线BF翻折，使点C落在矩形内部的一点C′处，且C′E∥BC，若点C′的坐标为（2，4），则tan∠CBF的值为．kx发布：2025/6/21 0:30:1组卷：4084引用：5难度：0.1
