如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P=90°，PM交AB于点E，PN交CD于点F．
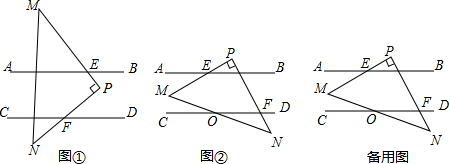
（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为∠PFD+∠AEM=90°∠PFD+∠AEM=90°．请说明理由作PG∥AB，如图①所示
则PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，作PG∥AB，如图①所示
则PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，．
（2）当△PMN所放位置如图②所示时，∠PFD与∠AEM的数量关系为∠PFD-∠AEM=90°∠PFD-∠AEM=90°．
（3）在（2）的条件下，若MN与CD交于点O，且∠DON=30°，∠PEB=15°，求∠N的度数．
则PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，
则PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，
【考点】平行线的性质．
【答案】∠PFD+∠AEM=90°；作PG∥AB，如图①所示
则PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，；∠PFD-∠AEM=90°
则PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，；∠PFD-∠AEM=90°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：860引用：4难度：0.8
相似题
-
1．如图，直线m∥n,若∠1=70°，则∠2的度数为（ ）发布：2025/6/13 17:30:5组卷：75引用：1难度：0.7 -
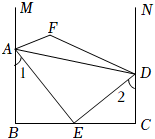2．黑板上有一个数学问题如图所示：
如图AB⊥BC，BC交CD于点C，AE平分∠BAD交BC于E，AE⊥DE，∠1+∠2=90°，M，N分别是BA，CD延长线上的点，∠EAM和∠EDN的平分线交于点F．
几位同学经过研究得到以下结论：
嘉嘉说：“AB∥CD”；
琪琪说：“∠AEB+∠ADC=180°”；
薇薇说：“DE平分∠ADC”；
亮亮说：“∠F=135°”，则（ ）发布：2025/6/13 20:0:1组卷：240引用：4难度：0.4 -
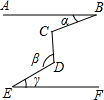3．已知：如图AB∥EF，BC⊥CD，则∠α，∠β，∠γ之间的关系是（ ）发布：2025/6/13 18:30:2组卷：2024引用：18难度：0.9
