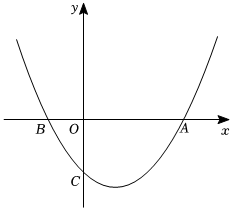
如图，在平面直角坐标系中，二次函数y=ax2-x+c的图象经过点A（6，0）、C（0，-3），点P为抛物线上y轴右侧一动点，其横坐标为m（m≥0），当点P不与该抛物线顶点重合时，过点P作y轴垂线交该抛物线于点E．
（1）求该抛物线对应的函数表达式．
（2）若此抛物线在点P右侧部分（包括点P）的最低点的纵坐标为2m-6时，求m的值．
（3）当∠OPE为锐角，且tan∠OPE＞1时，求m的取值范围．
（4）已知点M（m,m-3），点N（m-1，m-4），以MP、MN为邻边作▱PMNQ，当抛物线在▱PMNQ内部的部分的函数值y随x的增大而增大或y随x的增大而减少时，抛物线与▱PMNQ的边的交点的纵坐标之差为12时，直接写出m的值．
1
2
【考点】二次函数综合题．
【答案】（1）该抛物线对应的函数表达式为y=x2-x-3．
（2）m的值为1或6+2；
（3）当∠OPE为锐角，且tan∠OPE＞1时，m的取值范围2＜m＜2或 m＞4+2；
（4）m的值为或2-或或2+．
1
4
（2）m的值为1或6+2
6
（3）当∠OPE为锐角，且tan∠OPE＞1时，m的取值范围2＜m＜2
3
7
（4）m的值为
3
2
2
7
2
38
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/8 8:0:9组卷：174引用：1难度：0.2
相似题
-
1．如图，已知抛物线y=a（x+1）（x-3）交x轴于A、C两点，交y轴于B，且OB=2CO．
（1）求点A、B、C的坐标及二次函数解析式；
（2）假设在直线AB上方的抛物线上有动点E，作EG⊥x轴交x轴于点G，交AB于点M，作EF⊥AB于点F．若点M的横坐标为m,求线段EF的最大值；
（3）在抛物线的对称轴上是否存在点P使得△ABP为以AB为直角边的直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．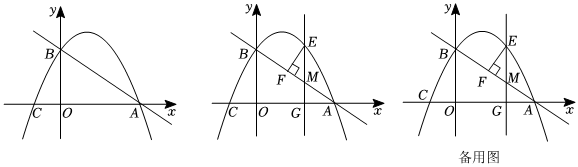
发布：2025/5/23 6:30:1组卷：258引用：3难度：0.2 -
2．如图，抛物线y=ax2+bx+c（a≠0）的图象经过A（1，0），（3，0），C（0，3）三点．
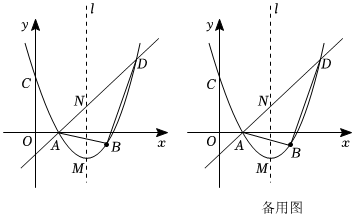
（1）求抛物线的解析式和顶点坐标．
（2）抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D，点B是直线AD下方抛物线上一动点，连接AB、BD，求出△ADB面积最大值．
（3）P为抛物线上的一动点，Q为对称轴上动点，抛物线上是否存在一点P，使A、D、P、Q为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．发布：2025/5/23 6:30:1组卷：73引用：1难度：0.5 -
3．如图1，在平面直角坐标系xOy中，已知抛物线y=-x2+bx+c经过A（-1，0），B（3，0）两点．P是抛物线上一点，且在直线BC的上方．
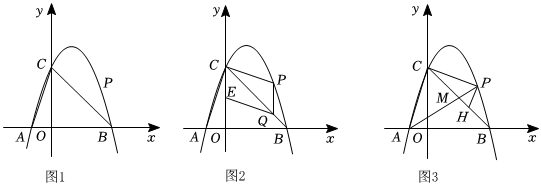
（1）求抛物线的解析式；
（2）如图2，点E为OC中点，作PQ∥y轴交BC于点Q，若四边形CPQE为平行四边形，求点P的横坐标；
（3）如图3，连结AC、AP，AP交BC于点M，作PH∥AC交BC于点H．记△PHM，△PMC，△CAM的面积分别为S1，S2，S3．判断是否存在最大值．若存在，求出最大值；若不存在，请说明理由．S1S2+S2S3发布：2025/5/23 6:0:2组卷：867引用：3难度：0.1
