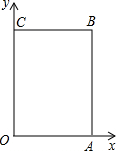
如图，在以点O为原点的平面直角坐标系中点A，B的坐标分别为（a,0），（a,b），点C在y轴上，且BC∥x轴，a,b满足|a-3|+b-4=0．点P从原点出发，以每秒2个单位长度的速度沿着O-A-B-C-O的路线运动（回到O为止）．
（1）直接写出点A，B，C的坐标；
（2）当点P运动3秒时，连接PC，PO，求出点P的坐标，并直接写出∠CPO，∠BCP，∠AOP之间满足的数量关系；
（3）点P运动t秒后（t≠0），是否存在点P到x轴的距离为12t个单位长度的情况．若存在，求出点P的坐标；若不存在，请说明理由．
b
-
4
1
2
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/31 8:0:9组卷：3097引用：15难度：0.5
相似题
-
1．如图所示，四边形ABCD是梯形，四边形OBCD是边长为1个单位长度的正方形，∠OAB=45°
（1）写出点A，B，C，D坐标；
（2）求梯形ABCD的面积．发布：2025/1/2 8:0:1组卷：58引用：1难度：0.7 -
2．已知点M（2a+5，a-2）在第四象限，分别根据下列条件求点M的坐标．
（1）点M到x轴的距离为3；
（2）点N的坐标为（5，-4），且直线MN与坐标轴平行．发布：2024/12/23 19:30:2组卷：1102引用：8难度：0.8 -
3．已知在平面直角坐标系中，点A的坐标为（a+2，3a-1）．
（1）若点A在y轴上，求出点A的坐标；
（2）点B的坐标为（3，5），若AB∥x轴，求出点A的坐标．发布：2024/12/23 19:30:2组卷：1805引用：12难度：0.6
