如图，在平面直角坐标系中，已知抛物线y=ax2-4交x轴于A、B两点，交y轴于点C，且AB=4．
（1）则a的值为 11；
（2）点P在第一象限的抛物线上，连接AP交y轴正半轴于点E，若点P的横坐标为t,CE长为d,求d与t的函数关系式；
（3）在y轴上另取一点D，D在点E的上方，过点D作x轴的平行线交AP的延长线于点G，连接AD、BG，若∠DAG=2∠BAG，AD：BG=5：61，求点P的坐标．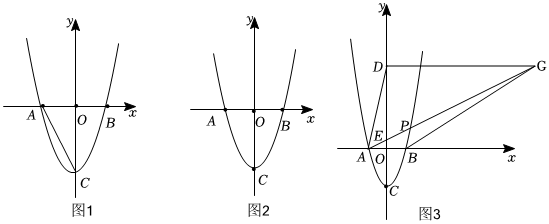
61
【考点】二次函数综合题．
【答案】1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/28 6:0:10组卷：79引用：1难度：0.1
相似题
-
1．如图，在平面直角坐标系中，抛物线y=-x2-2x+c（c为常数）与一次函数y=-x+b（b为常数）交于A、B两点，其中A点坐标为（-3，0）．
（1）求B点坐标；
（2）点P为直线AB上方抛物线上一点，连接PA，PB，当S△PAB=时，求点P的坐标；1258
（3）将抛物线y=-x2-2x+c（c为常数）沿射线AB平移5个单位，平移后的抛物线y1与原抛物线y=-x2-2x+c相交于点E，点F为抛物线y1的顶点，点M为y轴上一点，在平面直角坐标系中是否存在点N，使得以点E，F，M，N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．2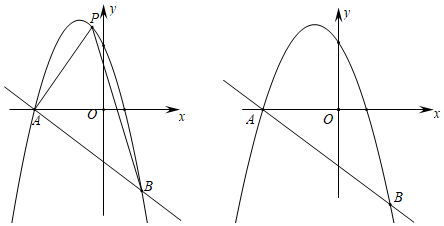
发布：2025/6/9 22:30:2组卷：485引用：5难度：0.1 -
2．在平面直角坐标系xOy中，抛物线y=x2+bx+c（b、c为常数）经过点A（0，-3）和点B（3，0），点M在此抛物线，点M的横坐标为m,点M不与A、B重合．
（1）求此抛物线所对应的函数表达式．
（2）当S△OAM=2S△AOB，求点M的坐标．
（3）作点A关于抛物线对称轴的对称点为点C，当点M到直线AC的距离是点M到x轴距离2倍时，求m的值．
（4）设点E的坐标为（-m-2，m），点F的坐标为（2m-2，m），连接EF．当抛物线在B、M两点之间的部分（包含B、M两点）与线段EF有1个公共点时，直接写出m的取值范围．发布：2025/6/9 23:30:1组卷：125引用：3难度：0.2 -
3．【生活情境】
为美化校园环境，某学校根据地形情况，要对景观带中一个长AD=4m,宽AB=1m的长方形水池ABCD进行加长改造（如图①，改造后的水池ABNM仍为长方形，以下简称水池1）．同时，再建造一个周长为12m的矩形水池EFGH（如图②，以下简称水池2）．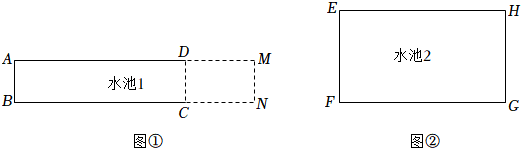
【建立模型】
如果设水池ABCD的边AD加长长度DM为x（m）（x＞0），加长后水池1的总面积为y1（m2），则y1关于x的函数解析式为：y1=x+4（x＞0）；设水池2的边EF的长为x（m）（0＜x＜6），面积为y2（m2），则y2关于x的函数解析式为：y2=-x2+6x（0＜x＜6），上述两个函数在同一平面直角坐标系中的图象如图③．
【问题解决】
（1）若水池2的面积随EF长度的增加而减小，则EF长度的取值范围是 （可省略单位），水池2面积的最大值是 m2；
（2）在图③字母标注的点中，表示两个水池面积相等的点是 ，此时的x（m）值是 ；
（3）当水池1的面积大于水池2的面积时，x（m）的取值范围是 ；
（4）在1＜x＜4范围内，求两个水池面积差的最大值和此时x的值；
（5）假设水池ABCD的边AD的长度为b（m），其他条件不变（这个加长改造后的新水池简称水池3），则水池3的总面积y3（m2）关于x（m）（x＞0）的函数解析式为：y3=x+b（x＞0）．若水池3与水池2的面积相等时，x（m）有唯一值，求b的值．发布：2025/6/10 0:0:1组卷：1987引用：6难度：0.3
