如图，点E为正方形ABCD内一点，∠AEB=90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBG．延长AE交CG于点F，连接DE．下列结论：①AF⊥CG，②四边形BEFG是正方形，③若DA=DE，则CF=FG；其中正确的结论是（ ）
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：1558引用：20难度：0.2
相似题
-
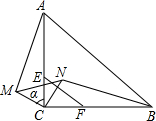1．如图，已知，在△ABC中，CA=CB，∠ACB=90°，E，F分别是CA，CB边的三等分点，将△ECF绕点C逆时针旋转α角（0°＜α＜90°），得到△MCN，连接AM，BN．
（1）求证：AM=BN；
（2）当MA∥CN时，试求旋转角α的余弦值．发布：2025/6/25 6:30:1组卷：2475引用：59难度：0.5 -
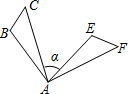2．如图，△ABC绕点A顺时针旋转80°得到△AEF，若∠B=100°，∠F=50°，则∠α的度数是．发布：2025/7/1 13:0:6组卷：1099引用：19难度：0.7 -
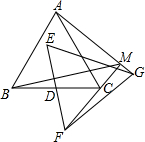3．如图，△ABC，△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最小值是（ ）发布：2025/6/25 6:0:1组卷：5913引用：58难度：0.5
