【初步探究】
（1）如图1，在四边形ABCD中，∠B=∠C=90°，E是边BC上一点，AB=EC，BE=CD，连接AE，DE．请你证明：EA=ED，∠AED=90°．
【问题解决】
（2）若设DE=c,CD=a,CE=b,试利用图1验证勾股定理．
【迁移应用】
（3）如图2，将一块等腰直角的三角板MON放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O重合，另两个顶点均落在第一象限内，已知点M的坐标为（1，3），求点N的坐标．
【拓展应用】
（4）如图3，在平面直角坐标系中，已知点A（2，0），点B（4，1），点C在第一象限内，若△ABC为等腰直角三角形，请直接写出点C的坐标．
【考点】四边形综合题．
【答案】（1）见解析；
（2）见解析；
（3）（4，2）；
（4）（1，2）或（3，3）或；
（2）见解析；
（3）（4，2）；
（4）（1，2）或（3，3）或
（
5
2
，
3
2
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/5 4:0:2组卷：152引用：3难度：0.5
相似题
-
1．将纸片△ABC沿DE折叠使点A落在点A'处．
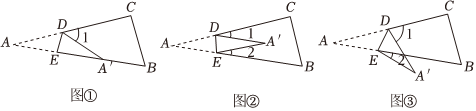
【感知】如图①，点A落在四边形BCDE的边BE上，则∠A与∠1之间的数量关系是 ；
【探究】如图②，若点A落在四边形BCDE的内部，则∠A与∠1+∠2之间的数量关系是 ；
【拓展】如图③，点A落在四边形BCDE的外部，若∠1=80°，∠2=24°，则∠A的大小为 ．发布：2025/6/17 4:30:1组卷：309引用：4难度：0.4 -
2．如图1，在Rt△ABC中，∠ACB=90°，∠CAB=30°，点D在边AB上以CD为底边作等腰直角△CDP（点P，A在直线CD的两侧），射线CP交直线AB于点E．
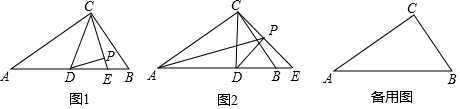
（1）若点D是AB的中点，且BC=2，求DP的长；
（2）当△CDE是等腰三角形时，求∠BCE的度数；
（3）如图2，设AP=a,求四边形ADPC面积的最小值．（用含a的式子表示）发布：2025/6/17 4:30:1组卷：26引用：1难度：0.4 -
3．如图，在菱形ABCD中，对角线AC，BD交于点O．
（1）若AB=5，AC=8，则菱形ABCD的面积是 ；
（2）点F在BC上，AF交BD于点E，若BE=BF，求证：CF=2OE；
（3）点P在射线AC上，且∠PDO=，若AC=16，AD=10，则DP的长为 ．12∠PCD
发布：2025/6/17 4:30:1组卷：164引用：2难度：0.1
