（1）方法回顾
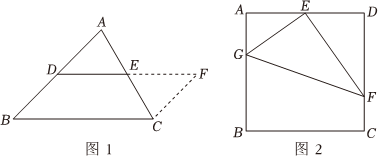
在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：第一步添加辅助线：如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF=DE，连接CF；
第二步证明△ADE≌△CFE（依据①SASSAS）易证，BD=CF，BD∥CF，再证四边形DBCF是平行四边形（依据②一组对边平行且相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形）
从而得到中位线DE与BC的关系：位置关系③DE∥BCDE∥BC，数量关系④DE=12BCDE=12BC；
（2）问题解决
如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG=2，AD=6，∠GEF=90°，求GF的长．
1
2
1
2
【答案】SAS；一组对边平行且相等的四边形是平行四边形；DE∥BC；DE=BC
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：43引用：1难度：0.5
相似题
-
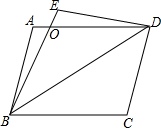1．在平行四边形ABCD中，将△BCD沿BD翻折，使点C落在点E处，BE和AD相交于点O，求证：OA=OE．发布：2025/6/19 12:30:1组卷：870引用：59难度：0.7 -
2．在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直线MN过点A且MN∥BC，过点B为一锐角顶点作Rt△BDE，∠BDE=90°，且点D在直线MN上（不与点A重合），如图1，DE与AC交于点P，易证：BD=DP．（无需写证明过程）
（1）在图2中，DE与CA延长线交于点P，BD=DP是否成立？如果成立，请给予证明；如果不成立，请说明理由；
（2）在图3中，DE与AC延长线交于点P，BD与DP是否相等？请直接写出你的结论，无需证明．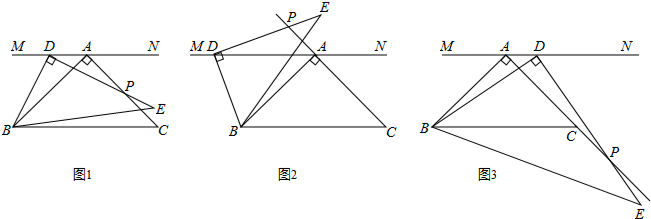
发布：2025/6/19 12:30:1组卷：3619引用：63难度：0.1 -
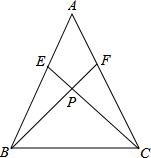3．在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点P．求证：PB=PC，并直接写出图中其他相等的线段．发布：2025/6/19 12:30:1组卷：1103引用：71难度：0.5
