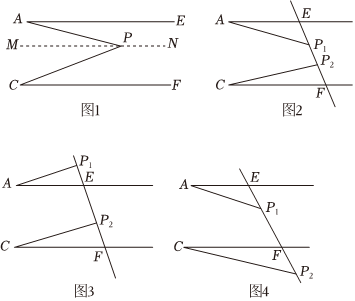
（1）已知：如图1，AE∥CF，易知∠APC=∠A+∠C，请补充完整证明过程：
证明：过点P作MN∥AE．
∵MN∥AE（已作）．
∴∠APM=∠A∠A（ 两直线平行，内错角相等两直线平行，内错角相等），
又∵AE∥CF，MN∥AE．
∴MN∥CF．
∴∠MPC=∠C∠C（ 两直线平行，内错角相等两直线平行，内错角相等）．
∴∠APM+∠CPM=∠A+∠C．
即∠APC=∠A+∠C．
（2）变式：AE∥CF，P1，P2是直线EF上的两点，猜想∠A，∠AP1P2，∠P1P2C，∠C这四个角之间的关系，并直接写出图2、图3、图4三种情况下这四个角之间的关系，并选一种关系说明理由．
【答案】∠A；两直线平行，内错角相等；∠C；两直线平行，内错角相等
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/3 8:0:9组卷：111引用：2难度：0.6
相似题
-
1．如图，D是AB上一点，E是AC上一点，∠ADE=60°，∠B=60°，∠AED=40°．
（1）DE和BC平行吗？
（2）∠C是多少度？为什么？发布：2025/1/23 8:0:2组卷：73引用：2难度：0.7 -
2．如图，D是AB上一点，E是AC上一点，∠ADE=65°，∠B=65°，∠AED=45°．求∠C的度数．发布：2025/1/23 8:0:2组卷：233引用：1难度：0.8 -
3．如图，∠ABC+∠ECB=180°，∠P=∠Q．
求证：∠1=∠2．
根据图形和已知条件，请补全下面这道题的解答过程．
证明：∵∠ABC+∠ECB=180° ，
∴AB∥ED ．
∴∠ABC=∠BCD ．
又∵∠P=∠Q（已知），
∴PB∥．
∴∠PBC=．
又∵∠1=∠ABC-，∠2=∠BCD-，
∴∠1=∠2（等量代换）．发布：2024/12/23 20:0:2组卷：1155引用：10难度：0.7
