如图1，AD∥BC，DE平分∠ADB，∠BDC=∠BCD．
（1）求证：∠DEC+∠ECD=90°；
（2）如图2，BF平分∠ABD交CD的延长线于点F，若∠ABC=100°，求∠F的大小；
（3）如图3，若H是BC上一动点，K是BA延长线上一点，KH交BD于点M，交AD于点O，KG平分∠BKH，交DE于点N，交BC于点G，当点H在线段BC上运动时（不与点B重合），求∠BAD+∠DMH∠DNG的值．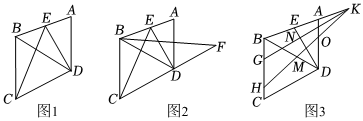 
∠
BAD
+
∠
DMH
∠
DNG
【考点】平行线的性质．
【答案】（1）证明见解答；
（2）∠F=40°；
（3）2．
（2）∠F=40°；
（3）2．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/28 19:0:9组卷：485引用：1难度：0.3
相似题
-
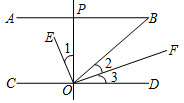1．如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=40°，则下列结论：①∠BOE=70°；②OF平分∠BOD；③∠1=∠2；④∠POB=2∠3．其中正确的结论有．（填序号）发布：2025/6/18 5:30:3组卷：429引用：8难度：0.8 -
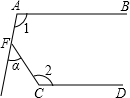2．如图，AB∥CD，∠1=100°，∠2=120°，则∠α等于（ ）发布：2025/6/18 5:30:3组卷：157引用：4难度：0.9 -
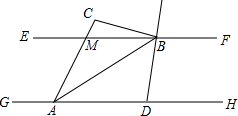3．已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=120°，则∠DBA的度数 ．发布：2025/6/18 5:30:3组卷：1317引用：3难度：0.5
