【阅读】求值1+2+22+23+24+…+210
解：设S=1+2+22+23+24+…+210①
将等式①的两边同时乘以2得：2S=2+22+23+24+25+…+211②
由②-①得：2S-S=211-1
即：S=1+2=22+23+24+…+210=211-1
【运用】仿照此法计算：
（1）1+3+32+33+34+…+350；
（2）1+12+122+123+…+12100
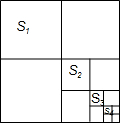
【延伸】如图，将边长为1的正方形分成4个完全一样的小正方形，得到左上角一个小正方形为S1，选取右下角的小正方形进行第二次操作，又得到左上角更小的正方形S2，依次操作2017次，依次得到小正方形S1、S2、S3、…S2017．
完成下列问题：
（3）小正方形S2017的面积等于142017142017；
（4）求正方形S1、S2、S3、…、S2017的面积和．
1
2
1
2
2
1
2
3
1
2
100
1
4
2017
1
4
2017
【考点】规律型：图形的变化类；有理数的混合运算．
【答案】
1
4
2017
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/13 16:0:8组卷：293引用：3难度：0.3
相似题
-
1．某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：
上述问题中，第五排、第六排分别有 个、个座位；第n排有 个座位．排数 1 2 3 4 … 座位数 50 53 56 59 … 发布：2025/6/15 5:0:1组卷：37引用：3难度：0.6 -
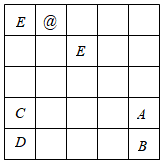2．如图，要在下列5×5的方格表中填入A、B、C、D、E五个英文字母，并且要求五个字母在每一行与每一列及对角在线，都只出现一次，则@所表示的英文字母为 ．发布：2025/6/17 0:30:1组卷：8引用：1难度：0.6 -
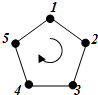3．如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．若小宇从编号为2的顶点开始，第81次“移位”后，则他所处顶点的编号是．发布：2025/6/16 22:30:4组卷：106引用：5难度：0.7
