已知直线AB∥CD,E为平面内一点,连接EB、EC.
(1)如图1,已知∠B=32°,∠C=120°,求∠BEC的度数;
(2)如图2,判断∠ABE、∠BEC、∠DCE之间的数量关系为 ∠ABE-∠BEC+∠DCE=180°∠ABE-∠BEC+∠DCE=180°;
(3)如图3,BE⊥CE,BF平分∠ABE,若∠ECF+12∠ECD=90°,求∠BFC的度数.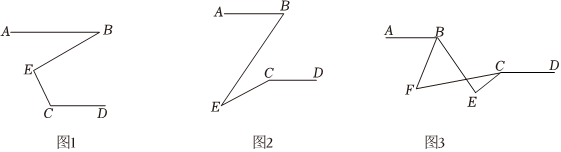
∠
ECF
+
1
2
∠
ECD
=
90
°
【答案】∠ABE-∠BEC+∠DCE=180°
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/19 8:0:9组卷:396引用:1难度:0.5