 阅读下列材料
阅读下列材料
利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式.
例如:x2-8x+17=x2-2•x•4+42-42+17=(x-4)2+1.
(1)填空:将多项式x2-2x+3变形为(x+m)2+n的形式,并判断x2-2x+3与0的大小关系.
∵x2-2x+3=(x-11)2+22.
所以x2-2x+3>>0(填“>”、“<”、“=”)
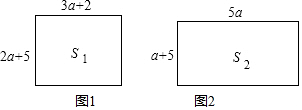
(2)如图①所示的长方形边长分别是2a+5、3a+2,求长方形的面积S1(用含a的式子表示);如图②所示的长方形边长分别是5a、a+5,求长方形的面积S2(用含a的式子表示)
(3)比较(2)中S1与S2的大小,并说明理由.
【考点】配方法的应用;非负数的性质:偶次方.
【答案】1;2;>
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/15 18:0:1组卷:739引用:7难度:0.6
相似题
-
1.比较x2+1与2x的大小.
(1)尝试(用“<”“=”或“>”填空):
①当x=1时,x2+1 2x;
②当x=0时,x2+1 2x;
③当x=-2时,x2+1 2x.
(2)归纳:若x取任意实数,x2+1与2x有怎样的大小关系?试说明理由.发布:2025/6/9 21:0:1组卷:1033引用:20难度:0.6 -
2.已知多项式M=2x2-3x-2.多项式N=x2-ax+3.
①若M=0,则代数式的值为13xx2-3x-1;263
②当a=-3,x≥4时,代数式M-N的最小值为-14;
③当a=0时,若M•N=0,则关于x的方程有两个实数根;
④当a=3时,若|M-2N+2|+|M-2N+15|=13,则x的取值范围是-<x<2.73
以上结论正确的个数是( )发布:2025/6/9 18:0:2组卷:669引用:5难度:0.4 -
3.阅读下面的材料:
【材料一】若m2-2mn+2n2-8n+16=0,求m,n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,
∴(m-n)2+(n-4)2=0,
∴(m-n)2=0,(n-4)2=0,
∴n=4,m=4.
【材料二】“a≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:m2+8m+17=m2+8m+16+1=(m+4)2+1.
∵(m+4)2≥0,
∴(m+4)2+1≥1,
∴m2+8m+17≥1.
故m2+8m+17有一个最小值为1.
阅读材料,探究下列问题:
(1)已知x2-2xy+2y2+6y+9=0,求xy的值;
(2)无论m取何值,代数式m2+6m+13总有一个最小值,求出它的最小值.发布:2025/6/9 11:30:1组卷:384引用:4难度:0.7


