如图，在矩形ABCD中，AB=8，AD=6，连结BD．点P从点A出发，沿折线AB-BD-DC以每秒1个单位长度的速度向终点C运动．当点P不与矩形ABCD的顶点重合时，以AP为对角线作正方形AEPF（点F在直线AP的右侧）．设正方形AEPF的面积为S（平方单位），点P的运动时间为t（秒）．
（1）当点P在线段BD上时，用含t的代数式表示PB的长；
（2）当AP⊥BD时，求t的值；
（3）求S与t之间的函数关系式．
【考点】四边形综合题．
【答案】（1）PB=t-8；
（2）t=或；
（3）S=
．
（2）t=
72
5
45
2
（3）S=
1 2 t 2 （ 0 ＜ t ＜ 8 ） |
1 2 t 2 - 72 5 t + 576 5 （ 8 ＜ t ＜ 18 ） |
1 2 t 2 - 18 t + 180 （ 18 ＜ t ＜ 26 ） |
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/31 8:0:9组卷：23引用：1难度：0.1
相似题
-
1．如图1，点O为矩形ABCD对角线AC的中点，AB=2，AD=2
．沿对角线AC将矩形剪开得到△ADC与△A′BC′，将△A′BC′绕点O逆时针旋转α°（0＜α≤120），记BC′与OC的交点为P，如图2．3
（1）①在图2中，连接OB，OD，BD，则△OBD的形状为 ；
②连接A′C，求证：A′C=BD；
（2）求OP长度的最小值；
（3）当△OPC′的内心在其一边的垂直平分线上时，直接写出α的值．
发布：2025/5/26 4:30:1组卷：83引用：2难度：0.3 -
2．已知，在▱ABCD中，E为AB上一点，且DE=2AD，作∠ADE的平分线交AB于点F．
（1）如图1，当E与B重合时，连接FC交BD于点G，若FC⊥CD，AF=3，求线段CF的长．
（2）如图2，当CE⊥AB时，过点F作FH⊥BC于点H，交EC于点M．若G为FD中点，CE=2AF，求证：CD-3AG=EM．
（3）如图3，在（1）的条件下，M为线段FC上一点，且CM=，P为线段CD上的一个动点，将线段MP绕着点M逆时针旋转30°得到线段MP′，连接FP′，直接写出FP′的最小值．3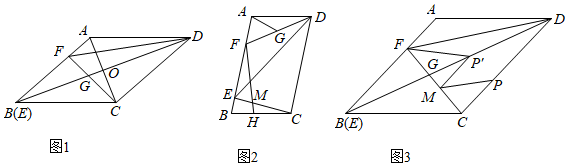
发布：2025/5/26 4:0:1组卷：481引用：2难度：0.1 -
3．如图，将矩形ABCD沿AF折叠，使点D落在BC边上的点E处，过点E作EG∥CD交AF于点G，连接DG．
（1）求证：四边形EFDG是菱形；
（2）探究线段EG、GF、AF之间的数量关系，并说明理由；
（3）若AG=6，EG=2，求BE的长．5发布：2025/5/26 5:0:1组卷：5059引用：11难度：0.1
