【阅读理解】
我们知道，1+2+3+…+n=n（n+1）2，那么12+22+32+…+n2结果等于多少呢？
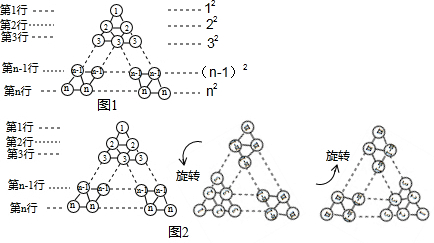
在图1所示三角形数阵中，第1行圆圈中的数为1，即12，第2行两个圆圈中数的和为2+2，即22，…；第n行n个圆圈中数的和为n个nn+n+…+n，即n2，这样，该三角形数阵中共有n（n+1）2个圆圈，所有圆圈中数的和为12+22+32+…+n2．
【规律探究】
将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n-1行的第一个圆圈中的数分别为n-1，2，n），发现每个位置上三个圆圈中数的和均为 2n+12n+1，由此可得，这三个三角形数阵所有圆圈中数的总和为：3（12+22+32+…+n2）=n（n+1）（2n+1）2n（n+1）（2n+1）2，因此，12+22+32+…+n2=n（n+1）（2n+1）6n（n+1）（2n+1）6．
【解决问题】
根据以上发现，计算：12+22+32+…+201721+2+3+…+2017的结果为 13451345．
n
（
n
+
1
）
2
n
个
n
n
+
n
+
…
+
n
n
（
n
+
1
）
2
n
（
n
+
1
）
（
2
n
+
1
）
2
n
（
n
+
1
）
（
2
n
+
1
）
2
n
（
n
+
1
）
（
2
n
+
1
）
6
n
（
n
+
1
）
（
2
n
+
1
）
6
1
2
+
2
2
+
3
2
+
…
+
201
7
2
1
+
2
+
3
+
…
+
2017
【考点】规律型：数字的变化类．
【答案】2n+1；；；1345
n
（
n
+
1
）
（
2
n
+
1
）
2
n
（
n
+
1
）
（
2
n
+
1
）
6
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/16 20:0:8组卷：2154引用：15难度：0.6
相似题
-
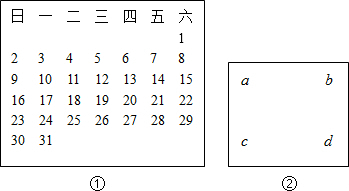
1．如图是①2011年10月日历，现用一长方形在日历中任意框出4个数如图②，请用一个等式表示a、b、c、d之间的关系：．
发布：2025/1/29 8:0:1组卷：56引用：2难度：0.7 -
2．法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的，后面的就改用手势了．右面两个图框是用法国“小九九”计算7×8和8×9的两个示例．若用法国“小九九”计算7×9，左、右手依次伸出手指的个数是（ ）发布：2024/12/5 8:0:1组卷：182引用：3难度：0.9 -
3．“数学是将科学现象升华到科学本质认识的重要工具”，比如在化学中，甲烷的化学式CH4，乙烷的化学式是C2H6，丙烷的化学式是C3H8，…，设碳原子的数目为n（n为正整数），则它们的化学式都可用下列哪个式子来表示（ ）
发布：2024/12/6 13:0:3组卷：247引用：5难度：0.5
