“厚德楼”、“博学楼”分别是我校两栋教学楼的名字，“厚德”出自《周易大传》：天行健，君子以自强不息；地势坤，君子以厚德载物．“博学”源自《论语•雍也》：君子博学于文，约之以礼．博学乃华夏古今治学之基础．我们不妨约定：在平面直角坐标系中，横、纵坐标相等的点称为“厚德点”，横、纵坐标互为相反数的点称为“博学点”．把函数图象至少经过一个“厚德点”和一个“博学点”的函数称为“厚德博学函数”．
（1）一次函数y=2x-1是一个“厚德博学函数”，分别求出该函数图象上的“厚德点”和“博学点”；
（2）已知二次函数y=a（x-h）2+k图象可以由二次函数y=-x2平移得到，二次函数y=a（x-h）2+k的顶点就是一个“厚德点”，并且该函数图象还经过一个“博学点”P（3，m），求该二次函数的解析式；
（3）已知二次函数y=2（x-c）2+d（c,d为常数，c≠0）图象的顶点为M，与y轴交于点N，经过点M，N的直线l上存在无数个“厚德点”．当m-1≤x≤m,函数y=2（x-c）2+d有最小值152，求m的值．
15
2
【考点】二次函数综合题．
【答案】（1）“厚德点”和“博学点”分别为：（1，1），（，-）；
（2）抛物线的表达式为：y=-（x-1）2+1或y=-（x-6）2+6；
（3）m=±．
1
3
1
3
（2）抛物线的表达式为：y=-（x-1）2+1或y=-（x-6）2+6；
（3）m=±
5
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/22 8:0:9组卷：531引用：1难度：0.3
相似题
-
1．已知：抛物线的解析式为y=x2-（2m-1）x+m2-m,
（1）求证：此抛物线与x轴必有两个不同的交点；
（2）若此抛物线与直线y=x-3m+4的一个交点在y轴上，求m的值．发布：2025/6/16 17:0:1组卷：621引用：37难度：0.1 -
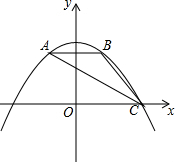2．如图，抛物线y=ax2+经过△ABC的三个顶点，点A坐标为（-1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．94
（1）求该抛物线的函数关系表达式；
（2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．发布：2025/6/16 19:30:1组卷：730引用：9难度：0.4 -
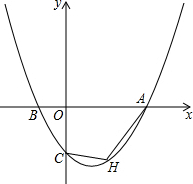3．如图，已知抛物线y=ax2+bx+c过点A（6，0），B（-2，0），C（0，-3）．
（1）求此抛物线的解析式；
（2）若点H是该抛物线第四象限的任意一点，求四边形OCHA的最大面积；
（3）若点Q在x轴上，点G为该抛物线的顶点，且∠QGA=45°，求点Q的坐标．发布：2025/6/16 23:0:1组卷：401引用：5难度：0.5
