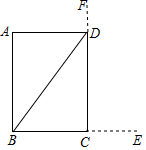
《九章算术》卷九“勾股”中记载：今有户不知高广，竿不知长短，横之不出四尺，纵之不出二尺，斜之适出，问户斜几何．
注：横放，竿比门宽长出四尺；竖放，竿比门高长出二尺，斜放恰好能出去．
解决下列问题：
（1）示意图中，线段CE的长为44尺，线段DF的长为22尺；
（2）求户斜多长．
【考点】勾股定理的应用．
【答案】4；2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/15 10:0:1组卷：339引用：2难度：0.5
相似题
-
1．已知三角形的三条边的长是三个连续的正整数，试讨论最小边长分别取什么值时，这个三角形是直角三角形、钝角三角形、锐角三角形？
发布：2025/5/27 21:30:2组卷：129引用：2难度：0.3 -
2．△ABC中，∠C=90°，a=5，c-b=l,试求b,c的长．
发布：2025/5/27 20:0:1组卷：77引用：3难度：0.7 -
3．一位无线电爱好者把天线杆设在接收效果最佳的矩形屋顶之上．然后，他从杆顶到屋顶四角之间安装固定用的支撑线．有两根相对的支撑线分别长7米和4米，另一根长1米，则最后一根的长度应为（ ）
发布：2025/5/27 20:30:1组卷：174引用：1难度：0.5
