细心观察图形，认真分析各式，然后解答问题：
OA1=1；
OA2=12+12=2；S1=12×1×1=12；
OA3=2+12=3；S2=12×2×1=22；
OA4=3+12=4；S3=12×3×1=32；
（1）推算出OA10=1010；
（2）用含n（n是正整数）的等式表示上述面积变化规律；
（3）求出S21+S22+S23+…+S2100的值．
1
2
+
1
2
=
2
；
S
1
=
1
2
×
1
×
1
=
1
2
2
+
1
2
3
1
2
×
2
×
1
2
2
3
+
1
2
4
1
2
×
3
3
2
10
10
S
2
1
S
2
2
S
2
3
S
2
100
【答案】
10
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/2 12:0:1组卷：72引用：1难度：0.5
相似题
-
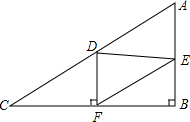1．如图，在Rt△ABC中，∠B=90°，AC=60，AB=30．D是AC上的动点，过D作DF⊥BC于F，过F作FE∥AC，交AB于E．设CD=x,DF=y.
（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当△DEF是直角三角形时，求x的值．发布：2025/6/24 21:30:1组卷：9218引用：64难度：0.3 -
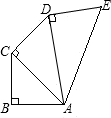2．如图所示，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（ ）发布：2025/7/1 13:0:6组卷：7900引用：52难度：0.9 -
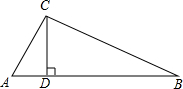3．如图，△ABC中，∠ACB=90°，AC=7，BC=24，CD⊥AB于D．
（1）求AB的长；
（2）求CD的长．发布：2025/6/24 21:0:1组卷：492引用：13难度：0.1
