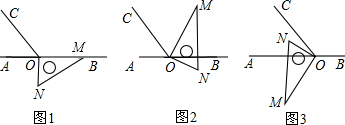
如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方，其中∠OMN=30°．
（1）将图1中的三角尺绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；
（2）将图1中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第 9或279或27秒时，边MN恰好与射线OC平行；在第 12或3012或30秒时，直线ON恰好平分锐角∠AOC．（直接写出结果）；
（3）将图1中的三角尺绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．
【考点】旋转的性质．
【答案】9或27；12或30
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：2502引用：14难度：0.3
相似题
-
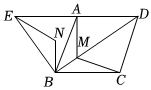1．如图，菱形ABCD中∠ABC=60°，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的个数是（ ）
①△AMB≌△ENB；
②若菱形ABCD的边长为2，则AM+CM的最小值2；
③连接AN，则AN⊥BE；
④当AM+BM+CM的最小值为时，菱形ABCD的面积也为43．43发布：2025/6/8 5:30:2组卷：150引用：3难度：0.3 -
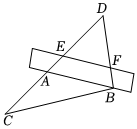2．如图，直尺经过一块三角板DCB的直角顶点B，∠C=30°，若将边BA从BC顺时针旋转，∠ABC=20°，则∠DEF度数为 °．发布：2025/6/8 4:0:1组卷：32引用：1难度：0.9 -
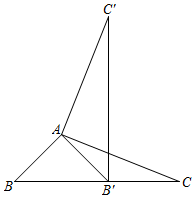3．如图，在△ABC中，∠BAC=117°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′刚好落在BC边上，且AB′=CB′，则∠C的度数为（ ）发布：2025/6/8 6:0:2组卷：334引用：3难度：0.7
