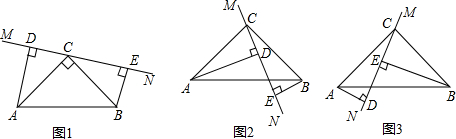
在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；
（2）当直线MN绕点C旋转到图2的位置时，直接写出DE、AD、BE的关系为：DE=AD-BEDE=AD-BE
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
【考点】全等三角形的判定与性质．
【答案】DE=AD-BE
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/10 1:0:9组卷：1601引用：6难度：0.3
相似题
-
1．已知△ABC是等腰直角三角形，∠BAC=90°，CD=
BC，DE⊥CE，DE=CE，连接AE，点M是AE的中点．12
（1）如图1，若点D在BC边上，连接CM，当AB=4时，求CM的长；
（2）如图2，若点D在△ABC的内部，连接BD，点N是BD中点，连接MN，NE，求证：MN⊥AE；
（3）如图3，将图2中的△CDE绕点C逆时针旋转，使∠BCD=30°，连接BD，点N是BD中点，连接MN，探索的值并直接写出结果．MNAC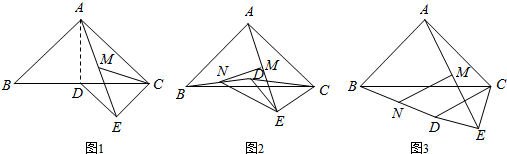
发布：2025/7/1 13:0:6组卷：2964引用：4难度：0.1 -
2．如图所示，在△ABC中，AB=AC，O是△ABC内一点，且OB=OC，AO的延长线交BC于点D．证明：BD=CD．发布：2025/7/1 13:0:6组卷：64引用：2难度：0.5 -
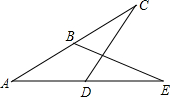3．如图，AD=AB，∠C=∠E，∠CDE=55°，则∠ABE=．发布：2025/7/1 13:0:6组卷：641引用：15难度：0.7
