【概念学习】规定：求若干个相同的有理数（均不等0）的除法运算叫做除方，如3÷3÷3，（-2）÷（-2）÷（-2）÷（-2）等．类比有理数的乘方，我们把3÷3÷3记作3^③，读作“3的圈3次方”，（-2）÷（-2）÷（-2）÷（-2）记作（-2）^④，读作“-2的圈4次方”．一般地，把
a
÷
a
÷
a
÷
•••
÷
a
n
个
（
a
≠
0
）
记作a^ⓝ，读作“a的圈n次方”．

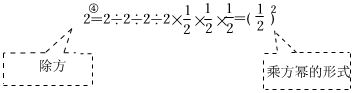
【初步探究】
（1）直接写出计算结果：4^③=
1
4
1
4
，
（
-
1
2
）
④
=
4
4
．
【深入思考】我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？（此处不用作答）
（2）试一试：仿照上面的算式，将下列运算结果直接写成乘方幂的形式（-3）^④=
（
-
1
3
）
2
（
-
1
3
）
2
；5^⑥=
（
1
5
）
4
（
1
5
）
4
；
（
1
2
）
⑤
=
2³
2³
．
（3）想一想：将一个非零有理数a的圈n次方写成乘方幂的形式等于
（
1
a
）
n
-
2
（
1
a
）
n
-
2
．
（4）比较：（-9）^⑤
＞
＞
（-3）^⑦（填“＞”“＜”或“=”）．
【灵活应用】
（5）算一算：
-
3
2
÷
（
-
1
3
）
⑤
×
（
-
1
4
）
④
．

【答案】

；4；

（

）

；

（

）

；2³；

（

）

；＞

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/10/24 17:0:5组卷：197引用：6难度：0.5

相似题

1．已知a,b互为相反数，c,d互为倒数，|x|=1，求
|
x
|
+
（
a
+
b
+
1
cd
）
-
cd
的值．
发布：2025/1/28 8:0:2组卷：70引用：1难度：0.5
解析
2．已知a、b互为相反数，c、d互为倒数，m是绝对值等于2的数，求：
a
+
b
a
+
b
+
c
+m³-cd的值．
发布：2025/1/28 8:0:2组卷：61引用：1难度：0.3
解析
3．已知：a、b互为相反数，c、d互为倒数，m的绝对值是5，则代数式2019（a+b）-3cd+2m的值为
．
发布：2025/1/28 8:0:2组卷：110引用：2难度：0.7
解析

1．已知a,b互为相反数，c,d互为倒数，|x|=1，求|x|+（a+b+1cd）-cd的值．