问题提出
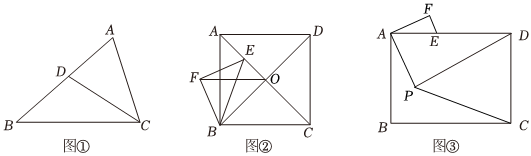
（1）如图①，已知△ABC，点D是AB上一点，且∠ACD=∠B，求证：AC2=AD•AB；
问题探究
（2）如图②，在正方形ABCD中，AB=4，对角线AC、BD相交于点O，点E是AO上一点，且OE=1，连接BE，以BE为斜边向左作等腰直角△BEF，连接OF，求OF的长；
问题解决
（3）如图③，矩形ABCD是某公园的平面示意图，已知AB=600米，BC=800米，点E是AD边上且距离公园D出口500米远的一个观测点，观测距离EF=100米．现计划在公园内部且与AF垂直的方向上修建一座凉亭P，要求AP=2AF．为了游客能更好的欣赏公园风景，在凉亭P和出口C、D之间需再修建两条观光小路PD和PC（小路宽度不计）．已知小路PD的造价为2000元/米．小路PC的造价为500元/米，请你根据题中提供的信息，求出修建观光小路的最低费用．
【考点】相似形综合题．
【答案】（1）证明见解答；
（2）2+；
（3）1.92×106元．
（2）2+
2
2
（3）1.92×106元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/29 5:0:4组卷：162引用：1难度：0.3
相似题
-
1．如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线ON上的两动点，点Q在点P的右侧，且PQ=OA，作线段OQ的垂直平分线，分别交直线OF、ON于点B、点C，连接AB、PB．
（1）如图1，当P、Q两点都在射线ON上时，请直接写出线段AB与PB的数量关系；
（2）如图2，当P、Q两点都在射线ON的反向延长线上时，线段AB，PB是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由；
（3）如图3，∠MON=60°，连接AP，设=k,当P和Q两点都在射线ON上移动时，k是否存在最小值？若存在，请直接写出k的最小值；若不存在，请说明理由．APOQ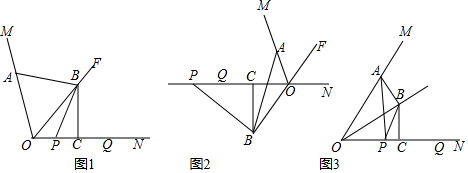
发布：2025/5/24 23:30:2组卷：2276引用：6难度：0.3 -
2．如图1，Rt△ABC中，∠A=90°，D为AB上一点，∠ACD=∠B．
（1）求证：AC2=AD•AB；
（2）如图2，过点A作AM⊥CD于M，交BC于点E，若，求CDBC=12的值；AMME
（3）如图3，N为CD延长线上一点，连接AN、BN，若，∠NBD=2∠ACD，则tan∠ANC的值为 ．CDBN=53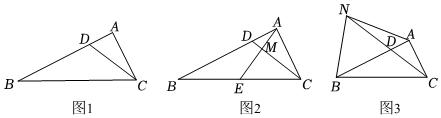
发布：2025/5/24 23:30:2组卷：239引用：1难度：0.3 -
3．【操作发现】
（1）如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．请按要求画图：将ABC绕点A顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′，此时∠ABB′=；
【问题解决】
在某次数学兴趣小组活动中，小明同学遇到了如下问题：
（2）如图2，在等边△ABC中，点P在内部，且PA=3，PC=4，∠APC=150°，求PB的长．
经过同学们的观察、分析、思考、交流、对上述问题形成了如下想法：将△APC绕点A按顺时针方向旋转60°，得到△ABP′，连接PP′，寻找PA、PB、PC三边之间的数量关系……请参考他们的想法，完成该问题的解答过程；
【学以致用】
（3）如图3，在等边△ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°．求△APC的面积；
【思维拓展】
如图4，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=1，CD=3，AD=kAB（k为常数），请直接写出BD的长（用含k的式子表示）．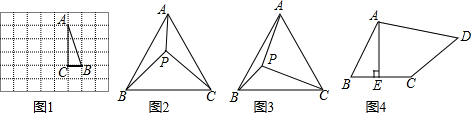
发布：2025/5/24 23:0:1组卷：789引用：2难度：0.2
