在平面直角坐标系xOy中:
(Ⅰ)若曲线C1,C2的方程分别为F1(x,y)=0、F2(x,y)=0,则由C1,C2组合构成的图形,其方程为F1(x,y)•F2(x,y)=0.例如,由直线y=x、y=-x组合构成的相交直线,其方程为(x-y)(x+y)=0,即:x2-y2=0.
请尝试说明,由方程:xy-1=x-y、x4=y2表示的图形,分别是哪两条曲线的组合?
(Ⅱ)若直线L1,L2相交,方程分别为a1x+b1y+c1=0、a2x+b2y+c2=0,则方程为(a1x+b1y+c1)(a2x+b2y+c2)=k的曲线是以L1,L2为渐近线的双曲线,其中k为非零常数.例如,以坐标轴为渐近线的双曲线,方程为xy=k(k≠0).
请尝试说明,函数y=x+1x的图象是双曲线,并指出其渐近线的方程.
y
=
x
+
1
x
【考点】反比例函数综合题.
【答案】(Ⅰ)xy-1=x-y,x4=y2表示的图形,分别是由直线x=-1和y=1组合,y=x2和y=-x2组合;
(Ⅱ)双曲线渐近线的方程为x=0和y=x.
(Ⅱ)双曲线渐近线的方程为x=0和y=x.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/7 0:0:8组卷:84引用:1难度:0.3
相似题
-
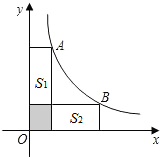 1.如图,点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=.3x发布:2025/6/15 18:0:1组卷:1568引用:124难度:0.7
1.如图,点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=.3x发布:2025/6/15 18:0:1组卷:1568引用:124难度:0.7 -
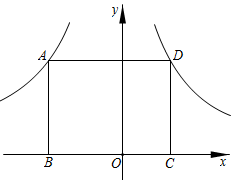 2.如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比例函数y=-和y=12x(m>0)的图象上.mx
2.如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比例函数y=-和y=12x(m>0)的图象上.mx
(1)当AB=BC时,求m的值;
(2)连接OA,OD.当OD平分∠AOC时,求△AOD的周长.发布:2025/6/16 11:0:1组卷:580引用:3难度:0.4 -
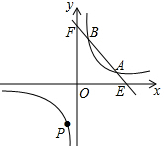 3.已知:一次函数y=-2x+10的图象与反比例函数y=(k>0)的图象相交于A,B两点(A在B的右侧).kx
3.已知:一次函数y=-2x+10的图象与反比例函数y=(k>0)的图象相交于A,B两点(A在B的右侧).kx
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.发布:2025/6/16 2:30:1组卷:459引用:2难度:0.4


