阅读以下材料，并按要求完成相应的任务：
| 等腰梯形 在第六章，我们按照“定义一性质一判定”的路径研究了平行四边形．生活中还有另一种特殊四边形一等腰梯形，我们可以类比平行四边形对其进行研究． 定义：只有一组对边平行的四边形叫做梯形，其中互相平行的两边叫做底，不平行的两边叫做腰．两腰相等的梯形叫做等腰梯形． 如图1，四边形ABCD是等腰梯形，其中AD∥BC，AB=DC． 性质：从整体对称性看，等腰梯形是轴对称图形： 从局部元素特征看，等腰梯形有如下性质： 性质1：等腰梯形同一底上的两个角相等；性质2：… 判定：与平行四边形类似，等腰梯形的性质与判定也具有互逆关系 判定1：…． |
（1）为证明等腰梯形的性质1，小颖的思考如下．请按她的思路选择一种方法写出证明过程．
已知：如图2，四边形ABCD是等腰梯形，AD∥BC，AB=DC．
求证：∠B=∠C，∠A=∠D．
证明：方法1：过点A作DC的平行线，交BC于点E，…；
方法2：过点A，D作BC的垂线，垂足分别为M，N，…．
（2）根据材料中的思路，小颖由等腰梯形的性质1得到关于等腰梯形判定方法的猜想，请你补全该命题，并判断其真假：
同一底上的两个角相等
同一底上的两个角相等
的梯形是等腰梯形，该命题是 真
真
命题．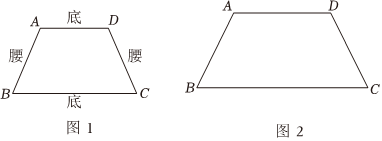
【考点】四边形综合题．
【答案】同一底上的两个角相等；真
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/15 8:0:9组卷：97引用：2难度：0.1
相似题
-
1．（1）如图1，在四边形ABCD中，∠ABC=∠ADC=90°，AD=CD，对角线BD=8，求四边形ABCD的面积；
（2）如图2，园艺设计师想在正六边形草坪一角∠BOC内改建一个小型的儿童游乐场OMAN．其中OA平分∠BOC，OA=100米，∠BOC=120°，点M，N分别在射线OB和OC上，且∠MAN=90°，为了尽可能的少破坏草坪，要使游乐场OMAN面积最小，你认为园林规划局的想法能实现吗？若能，请求出游乐场OMAN面积的最小值；若不能，请说明理由．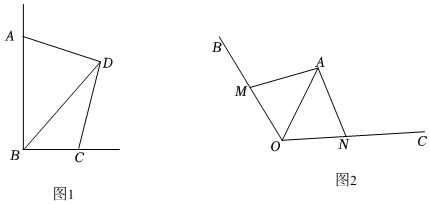
发布：2025/6/9 15:0:1组卷：243引用：2难度：0.2 -
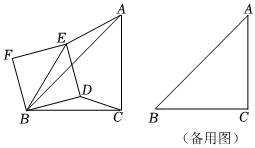2．如图，在Rt△ABC中，AC=BC=4，∠ACB=90°，正方形BDEF的边长为2，将正方形BDEF绕点B旋转一周，连接AE、BE、CD．
（1）请判断线段AE和CD的数量关系，并说明理由；
（2）当A、E、F三点在同一直线上时，求CD的长；
（3）设AE的中点为M，连接FM，试求线段FM长的取值范围．发布：2025/6/9 15:0:1组卷：209引用：1难度：0.1 -
3．[阅读理解]
“倍长中线”是初中数学一种重要的思想方法．如图1，在△ABC中，AD是BC边上的中线，若延长AD至E，使DE=AD，连接CE，可根据SAB证明△ABD≌△ECD，则AB=EC．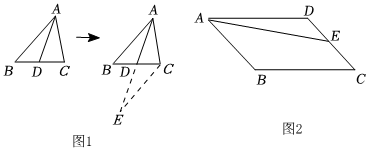
[问题提出]
（1）如图2，平行四边形ABCD中，点E为CD边的中点，在BC边上找一点F，使得AF=AD+CF（要求：用直尺和圆规作图，保留作图痕迹，不写作法）．
（2）按照你（1）中的作图过程证明：AF=AD+CF．发布：2025/6/9 15:30:2组卷：265引用：3难度：0.1
