如图是某月的日历，现有一个十字形框框出5个数，请观察图形解答下列问题：
（1）日历图中十字形框框出的5个数之和是该十字形框正中间数的 55倍；
（2）如果用a表示正中间的数，这5个数的和等于 5a5a，这个关系对其他这样的十字形框成立吗？
（3）这个关系对任何一个月的日历都成立吗？为什么？
（4）如果将十字形框改为H形框，你能发现哪些规律？
（5）你还能设计一个什么形状的包含数字规律的数框？
【考点】一元一次方程的应用；规律型：图形的变化类．
【答案】5；5a
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/17 13:0:5组卷：115引用：1难度：0.6
相似题
-
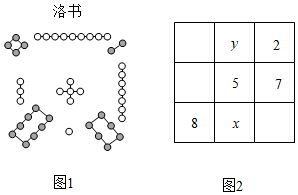
1．把1～9这九个数填入3×3方格中，使其任意一行，任意一列及任意一条对角线上的数之和都相等，这样便构成了一个“九宫格”，它源于我国古代的“洛书”（图1），是世界上最早的“幻方”．图2是仅可以看到部分数值的“九宫格”，则“x”的值为 ．发布：2025/5/23 4:30:1组卷：131引用：4难度：0.7 -
2．把1～9这九个数填入3×3方格中，使其任意一行，任意一列及任意一条对角线上的数之和都相等，这样便构成了一个“九宫格”，它源于我国古代的“洛書”（图1），是世界上最早的“幻方”．图2是仅可以看到部分数值的“九宫格”，则xy的值为 ．
发布：2025/5/23 5:0:2组卷：259引用：2难度：0.7 -
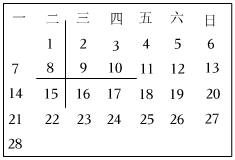3．如图是2022年2月的日历表：
（1）在图中用优美的“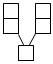
”U形框框住五个数，其中最小的数为1，则U形框中的五个数字之和为 ；
（2）在图中将U形框上下左右移动，框住日历表中的5个数字，设最小的数字为x,用代数式表示U形框框住的五个数字之和为 ；
（3）在图中移动U形框的位置，框住的五个数字之和可以为63吗？若能，求出这五个数字中最小的数；若不能，请说明理由．发布：2025/5/22 23:30:1组卷：174引用：1难度：0.6
