等腰直角△ABC中，∠BAC=90°，AB=AC，∠ABC=∠C，点B、A分别是x轴，y轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E．
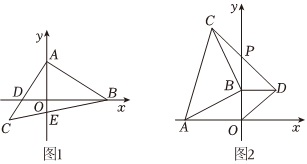
（1）如图1，已知C点的横坐标为-2，直接写出点A点的坐标；
（2）如图2，若点A为x轴上的固定点，且A（-6，0），当点B在y轴正半轴运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连接CD交y轴于点P，问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由；若不变化，请求出BP的长度．
【答案】（1）（2）BP的长度不变，理由见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/16 9:0:1组卷：32引用：1难度：0.5
相似题
-
1．如图，在∠AOB的两边上截取OC=OD，连接AD、BC交于点P．若∠A=∠B，则下列结论：①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．其中正确的是（ ）发布：2025/6/17 12:0:1组卷：118引用：4难度：0.7 -
2．如图，AB∥CD，AD和BC相交于点O，OA=OD．求证：OB=OC．发布：2025/6/17 12:30:1组卷：824引用：4难度：0.5 -
3．如图，已知BE⊥AC于点E，CF⊥AB于点F，BE，CF相交于点D，连接AD，BD=CD．求证：AD平分∠BAC．王刚的做法如下：
证明：∵BE⊥AC，CF⊥AB，BD=CD，
∴点D在∠BAC的平分线上，∴AD平分∠BAC．
王刚的做法正确吗？若不正确，请写出正确的证明过程．发布：2025/6/17 12:0:1组卷：62引用：1难度：0.7
