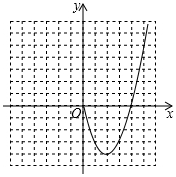
（1）课外学习小组根据学习函数的经验，对函数y=x2-4|x|的图象与性质进行了探究，请补充完整以下探索过程．
（1）列表：
| x | ⋯ | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ⋯ |
| y | ⋯ | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | ⋯ |
5
5
，n=-3
-3
；（2）根据上表中的数据，在平面直角坐标系内补全该函数的图象，并结合图象写出该函数的两条性质：
性质1：
函数图象关于y轴对称；
函数图象关于y轴对称；
；性质2：
函数有最小值-4．
函数有最小值-4．
．（3）请结合你所画的函数图象，写出方程x2-4|x|=-3的解为
x1=2+，x2=-2-
7
7
x1=2+，x2=-2-
．7
7
【答案】5；-3；函数图象关于y轴对称；；函数有最小值-4．；x1=2+，x2=-2-
7
7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 6:0:10组卷：16引用：1难度：0.5
相似题
-
1．已知直线l1：y=-2x+10交y轴于点A，交x轴于点B，二次函数的图象过A，B两点，交x轴于另一点C，BC=4，且对于该二次函数图象上的任意两点P1（x1，y1），P2（x2，y2），当x1＞x2≥5时，总有y1＞y2．
（1）求二次函数的表达式；
（2）直线l2：y=kx-5k+12与抛物线交于M、N两点，求△MNB面积的最小值．发布：2025/6/17 6:30:2组卷：157引用：1难度：0.1 -
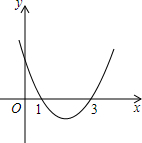2．如图，对称轴平行于y轴的抛物线与x轴交于（1，0），（3，0）两点，则它的对称轴为直线．发布：2025/6/17 7:30:2组卷：276引用：6难度：0.7 -
3．已知抛物线y=-x2+2（k-1）x+k+1与x轴交于A，B两点，且A点在x轴的正半轴上，B点在x轴的负半轴上．
（1）求抛物线的顶点坐标和对称轴方程．（用k表示）
（2）求k的取值范围．
（3）若=3，求k的值，并写出此时抛物线的解析式．OABO发布：2025/6/17 4:0:1组卷：72引用：3难度：0.3
