如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥DC于点F，连接EF，给出下列四个结论：①AP=EF；②AP⊥EF；③∠PFE=∠BAP；④PD=2EC，其中正确的是（ ）
2
【考点】正方形的性质；全等三角形的判定与性质．
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：925引用：6难度：0.6
相似题
-
1．正方形具有而菱形不具有的性质是（ ）
发布：2025/6/19 1:0:1组卷：776引用：25难度：0.9 -
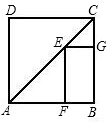2．如图，E是正方形ABCD对角线AC上一点，EF⊥AB，EG⊥BC，F、G是垂足，若正方形ABCD周长为a,则EF+EG等于（ ）发布：2025/6/19 1:0:1组卷：217引用：4难度：0.9 -
3．（1）如图（1）点P是正方形ABCD的边CD上一点（点P与点C，D不重合），点E在BC的延长线上，且CE=CP，连接BP，DE．求证：△BCP≌△DCE；
（2）在（1）条件下，直线EP交AD于F，连接BF，FC．点G是FC与BP的交点．
①若CD=2PC时，求证：BP⊥CF；
②若CD=n•PC（n是大于1的实数）时，记△BPF的面积为S1，△DPE的面积为S2．求证：S1=（n+1）S2．
发布：2025/6/18 21:0:1组卷：439引用：64难度：0.5
