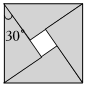
“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，若直角三角形其中的一个锐角为30°，一枚飞镖任意掷到如图所示的纸板上，则飞镖落在阴影区域的概率为 3232．
3
2
3
2
【答案】
3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/25 8:0:9组卷：39引用：1难度：0.5
相似题
-
1．小颖为九年级毕业晚会设计了一个“配紫色”的游戏，下图是两个可以自由转动的转盘，一个转盘被分成面积相等的三个扇形，另一个转盘被分成面积相等的两个半圆形，游戏者同时转动两个转盘，两个转盘停止转动时，若有一个转盘的指针指向蓝色，另一个转盘的指针指向红色，则“配紫色”成功，游戏者获胜，则游戏者获胜的概率是．
发布：2025/6/22 20:30:1组卷：76引用：2难度：0.7 -
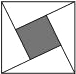2．“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4．小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是（ ）发布：2025/6/23 7:0:1组卷：287引用：37难度：0.7 -
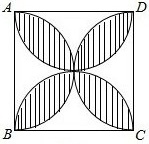3．正方形ABCD的边长为2，以各边为直径在正方形内画半圆，得到如图所示阴影部分，若随机向正方形ABCD内投一粒米，则米粒落在阴影部分的概率为．发布：2025/6/22 21:0:10组卷：281引用：4难度：0.5
相关试卷
