（1）如图，已知Rt△ABC中，∠ACB=90°，O是AB上一点．求作⊙O，使得⊙O过点A，且与BC相切．
要求：①用直尺和圆规作图；
②保留作图痕迹，写出必要的文字说明；
（2）如图，在Rt△ABC中，∠ACB=90°，∠CBA=30°，AC=1，D是边AB上一点（点D与点A不重合）．若在Rt△ABC的直角边上存在不同的点分别和点A、D构成直角三角形，直接写出不同的点的个数及对应的AD的长的取值范围．
【考点】圆的综合题．
【答案】（1）见解析；
（2）当存在2个点时，；
当存在3个点时，；
当存在4个点时，；
当存在1个点时，AD=2．
（2）当存在2个点时，
0
＜
AD
＜
4
3
当存在3个点时，
AD
=
4
3
当存在4个点时，
4
3
＜
AD
＜
2
当存在1个点时，AD=2．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/20 9:0:9组卷：213引用：1难度：0.5
相似题
-
1．如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．
（1）试说明CE是⊙O的切线；
（2）若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB；
（3）设点D是线段AC上任意一点（不含端点），连接OD，当CD+OD的最小值为6时，求⊙O的直径AB的长．12发布：2025/6/23 17:30:1组卷：4522引用：9难度：0.1 -
2．某地质公园为了方便游客，计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB，其中AC⊥BC，同时为减少对地质地貌的破坏，设立一个圆形保护区⊙M（如图所示），M是OA上一点，⊙M与BC相切，观景台的两端A、O到⊙M上任意一点的距离均不小于80米．经测量，OA=60米，OB=170米，tan∠OBC=．43
（1）求栈道BC的长度；
（2）①设OM=x,圆形保护区⊙M的半径为y,求y关于x的函数关系式，并求出自变量x的取值范围；
②当点M位于何处时，可以使该圆形保护区的面积最大？发布：2025/6/23 15:0:2组卷：41引用：1难度：0.3 -
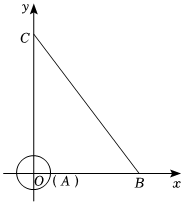3．如图，在平面直角坐标系中，半径为1的⊙A的圆心与坐标原点O重合，线段BC的端点分别在x轴与y轴上，点B的坐标为（6，0），且sin∠OCB=．35
（1）若点Q是线段BC上一点，且点Q的横坐标为m.
①求点Q的纵坐标；（用含m的代数式表示）
②若点P是⊙A上一动点，求PQ的最小值；
（2）若点A从原点O出发，以1个单位/秒的速度沿折线OBC运动，到点C运动停止，⊙A随着点A的运动而移动．
①点A从O→B的运动的过程中，若⊙A与直线BC相切，求t的值；
②在⊙A整个运动过程中，当⊙A与线段BC有两个公共点时，直接写出t满足的条件．发布：2025/6/23 14:0:1组卷：334引用：5难度：0.1
