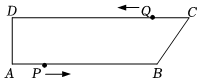
如图，在四边形ABCD中，AB∥CD，∠A=90°，AD=2cm,AB=10cm,CD=12cm.点P从点A出发，以1cm/s的速度向点B运动；点Q从点C出发，以x cm/s的速度向点D运动．规定其中一个点到达终点时，另一点也随之停止运动，设点Q的运动时间为t s,P，Q两点同时出发．
（1）若存在某一时刻，四边形APQD为正方形，求x的值；
（2）当x=2时，若PQ=BC，求t的值．
【考点】正方形的性质．
【答案】（1）x=2；
（2）t的值为或．
（2）t的值为
10
3
14
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/22 16:0:8组卷：154引用：1难度：0.6
相似题
-
1．如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．
发布：2025/6/19 20:30:1组卷：13312引用：85难度：0.5 -
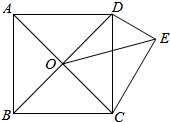2．如图，ABCD为正方形，O为AC、BD的交点，△DCE为Rt△，∠CED=90°，∠DCE=30°，若OE=，则正方形的面积为（ ）6+22发布：2025/6/19 20:0:1组卷：3690引用：62难度：0.5 -
3．如图，四边形ABCD，AEFG都是正方形，点E，G分别在AB，AD上，连接FC，过点E作EH∥FC交BC于点H．若AB=4，AE=1，则BH的长为（ ）发布：2025/6/19 20:0:1组卷：2137引用：65难度：0.9
