阅读下面的文字，完成后面的问题：
我们知道：11×2=1-12；12×3=12-13；13×4=13-14．
那么：
（1）14×5=14-1514-15；12019×2020=12019-1202012019-12020；
（2）用含有n的式子表示你发现的规律 1n（n+1）=1n-1n+11n（n+1）=1n-1n+1；
（3）求式子11×2+12×3+13×4+…+12019×2020的值．
1
1
×
2
1
2
1
2
×
3
1
2
1
3
1
3
×
4
1
3
1
4
1
4
×
5
1
4
-
1
5
1
4
-
1
5
1
2019
×
2020
1
2019
-
1
2020
1
2019
-
1
2020
1
n
（
n
+
1
）
=
1
n
-
1
n
+
1
1
n
（
n
+
1
）
=
1
n
-
1
n
+
1
1
1
×
2
1
2
×
3
1
3
×
4
1
2019
×
2020
【答案】；；
1
4
-
1
5
1
2019
-
1
2020
1
n
（
n
+
1
）
=
1
n
-
1
n
+
1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：521引用：6难度：0.5
相似题
-
1．如图，在数轴上，A1、P两点表示的数分别为1、2，若A1、A2关于O对称，A2、A3关于点P对称，A3、A4关于点O对称，A4、A5关于点P对称……依此规律，则点A2022表示的数是 ．
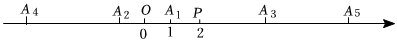发布：2025/6/9 3:30:1组卷：170引用：1难度：0.7 -
2．如图所示的运算程序中，若开始输入的x值为15，则第1次输出的结果为18，第2次输出的结果为9，……，第2022次输出的结果为（ ）
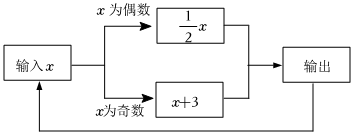发布：2025/6/9 5:30:2组卷：428引用：5难度：0.5 -
3．观察下面的一列单项式：x,-2x2，3x3，-4x4，…根据你发现的规律，第2022个单项式为 ；第n个单项式为 ．
发布：2025/6/9 3:30:1组卷：38引用：2难度：0.6
