在数学活动课上，老师出示了如下问题：
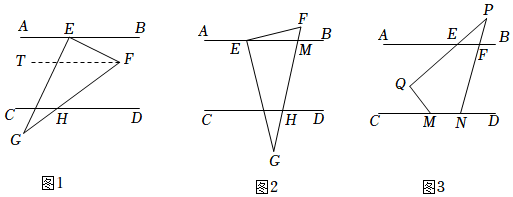
如图1，已知直线AB∥CD，将三角形纸片EFG的顶点E放到直线AB上，点F落在直线AB与CD所夹区域的内部，FG与CD交于点H，试探究∠EFH，∠BEF，∠DHF之间的数量关系．“兴趣小组”了如下探究思路：
过点F作FT∥AB．因为AB∥CD，∴FT∥CD．
∴∠BEF=∠TFE，……
数学思考
（1）请你根据“兴趣小组”的探究思路，直接写出∠EFH，∠BEF，∠DHF之间的数量关系：∠EFH=∠BEF+∠DHF∠EFH=∠BEF+∠DHF．
问题解决
（2）“智慧小组”把老师提出的问题作了如下变式：将三角形纸片EFG如图2所示放置，使得点F落在AB，CD区域的外部，FG与AB，CD分别交于点M，H．试探究∠EFH，∠BEF，∠DHF之间的数量关系．
请你类比“兴趣小组”的探究思路，解决智慧小组提出的问题．
结论运用
（3）如图3，直线AB∥CD，∠PND=75°，∠EPF=35°，∠PQM=95°．请你运用问题（1），（2）得到的结论，求∠QMC的度数．
【考点】平行线的判定与性质．
【答案】∠EFH=∠BEF+∠DHF
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：106引用：3难度：0.7
相似题
-
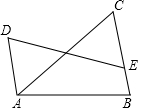1．如图，已知∠B+∠DAB=180°，AC平分∠DAB，如果∠C=50°，那么∠B等于（ ）发布：2025/6/17 13:30:1组卷：318引用：7难度：0.6 -
2．如图1，A、B分别是直线a和b上的点，∠1=∠2，C、D在两条直线之间，且∠C=∠D．
（1）证明：a∥b；
（2）如图2，∠EFG=60°，EF交a于H，FG交b于I，HK∥FG，若∠4=2∠3，判断∠5、∠6的数量关系，并说明理由；
（3）如图3，∠EFG是平角的n分之1（n为大于1的整数），FE交a于H，FG交b于I．点J在FG上，连接HJ．若∠8=n∠7，则∠9：∠10=．
发布：2025/6/17 14:30:2组卷：229引用：2难度：0.4 -
3．给出下列说法：
（1）两条直线被第三条直线所截，同位角相等；
（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；
（3）相等的两个角是对顶角；
（4）三条直线两两相交，有三个交点；
（5）若a⊥b,b⊥c,则a⊥c.
其中正确的有个．发布：2025/6/17 14:30:2组卷：85引用：1难度：0.7
