把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的式子，或可以求出一些不规则图形的面积．
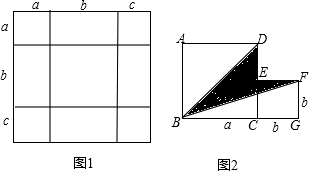
（1）如图1，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形．
①若用不同的方法计算这个边长为a+b+c的正方形面积，就可以得到一个等式，这个等式可以为 （a+b+c）（a+b+c）2=a2+b2+c2+2ab+2bc+2aca2+b2+c2+2ab+2bc+2ac．
②因式分解：a2+4b2+9c2+4ab+12bc+6ca.
（2）如图2，是将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF，若两正方形的边长满足a+b=6，ab=8，请求出阴影部分的面积．
【考点】完全平方公式的几何背景；因式分解-分组分解法．
【答案】（a+b+c）；a2+b2+c2+2ab+2bc+2ac
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：318引用：2难度：0.3
相似题
-
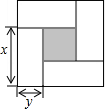1．如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案，已知该图案的面积为49，小正方形的面积为4，若分别用x,y（x＞y）表示小长方形的长和宽，则下列关系式中不正确的是（ ）发布：2025/5/26 12:0:1组卷：1033引用：8难度：0.7 -
2．如图，有两个正方形纸板A，B，纸板A与B的面积之和为34．现将纸板B按甲方式放在纸板A的内部，阴影部分的面积为4．若将纸板A，B按乙方式并列放置后，构造新的正方形，则阴影部分的面积为（ ）
发布：2025/5/26 7:30:2组卷：414引用：8难度：0.6 -
3．如图，将四个小正方形用两种不同方法放在大正方形的四个顶点，则图2中阴影部分的面积为（ ）发布：2025/5/25 16:0:2组卷：100引用：1难度：0.7
