如图，△ABC内接于⊙O，AB是⊙O的直径，过点A的切线交BC的延长线于点D，E是⊙O上一点，点C，E分别位于直径AB异侧，连接AE，BE，CE，∠ADB=∠DBE．
（1）求证：CE=CB；
（2）过点C作CF⊥AB，垂足为点F，若S△BCFS△ABE=98，求AFBF的值．
S
△
BCF
S
△
ABE
=
9
8
AF
BF
【考点】圆的综合题．
【答案】（1）见解析；
（2）．
（2）
5
9
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/23 8:0:8组卷：332引用：1难度：0.3
相似题
-
1．已知在△ABC中，⊙O为△ABC的外接圆，E为
的中点，过E作EF⊥直线AB，垂足为F．ˆBAC
（1）如图1，若AC＞AB，线段AC，AB、AF的关系为 ；
（2）如图2，若AB＞AC，探求线段AC，AB、AF的关系；
（3）如图3，在（2）的条件下，若∠B+∠C=120°，AC=10，AF=3，求⊙O的面积．
发布：2025/6/20 9:0:1组卷：154引用：1难度：0.1 -
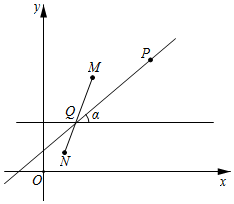2．在平面直角坐标系xOy中，对于线段MN和点P．给出如下定义：若在线段MN上存在点Q，过点Q作y轴的垂线l,使得直线PQ与直线l所形成的角中，有一个角为α（0°＜α≤90°），则称点P是线段MN的“α-联络点”．特别地，当PQ与直线l重合时，记α=0°，此时点P是线段MN的“0°-联络点”．
如图是线段MN的一个“α-联络点”的示意图．
已知点A（0，3），
（1）点B在直线x=3上，
①若点B的坐标为（3，-3），且它是线段OA的“α-联络点”，在α=30°和α=45°中，可能的α值为 ．
②若点B既是线段OA的“45°-联络点”，又是线段OA的“60°-联络点”．写出一个符合题意的点B的坐标；
（2）已知图形G是边长为a的等边三角形，若图形G上所有的点都是线段OA的“45°-联络点”，求a的最大值；
（3）⊙T的圆心为（t,0），直径为1，点M，N在以A为圆心，2为半径的圆上，且MN=2，若⊙T上所有的点都是线段MN的“45°-联络点”，直接写出t的取值范围．发布：2025/6/20 3:30:1组卷：99引用：1难度：0.2 -
3．在平面直角坐标系xOy中，对于△ABC，点P在BC边的垂直平分线上，若以点P为圆心，PB为半径的⨀P与△ABC三条边的公共点个数之和不小于3，则称点P为△ABC关于边BC的“Math点”．如图所示，点P即为△ABC关于边BC的“Math点”．已知点P（0，4），Q（a,0）．
（1）如图1，a=4，在点A（1，0）、B（2，2）、C（，23）、D（5，5）中，△POQ关于边PQ的“Math点”为．23
（2）如图2，，a=43
①已知D（0，8），点E为△POQ关于边PQ的“Math点”，请直接写出线段DE的长度的取值范围；
②将△POQ绕原点O旋转一周，直线交x轴、y轴于点M、N，若线段MN上存在△POQ关于边PQ的“Math点”，求b的取值范围．y=-3x+b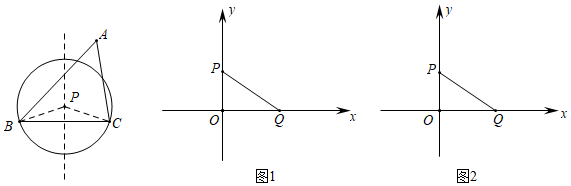
发布：2025/6/20 4:0:1组卷：559引用：4难度：0.1
