【教材呈现】如图是华师版七年级下册数学教材第77页的部分内容．

现在我们讨论三角形的外角及外角和． 如图9.1.9、一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角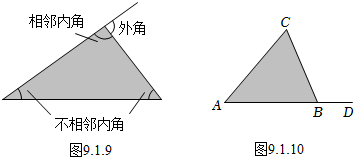． 三角形的外角与内角有什么关系呢？ 在图9.1.10中、显然有∠CBD（外角）+∠ABC（相邻的内角）=180°． 那么外角∠CBD与其他两个不相邻的内角又有什么关系呢？ 依据三角形的内角和等于180°，我们有∠ACB+∠BAC+∠ABC=180°． 由上面两个式子，可以推出： ∠CBD=180°-∠ABC． ∠ACB+∠BAC=180°-∠ABC． 因而可以得到你与你的同伴所发现的结论： ∠CBD=∠ACB+∠BAC． 由此可知，三角形的外角有两条性质： 1．三角形的一个外角等于与它不相邻的两个内角的和； 2．三角形的一个外角大于任何一个与它不相邻的内角．

【感知】如图①，在四边形AEFC中，EB、FD分别是边AE、CF的延长线，我们把∠BEF、∠DFE称为四边形AEFC的外角，若∠A+∠C=260°，则∠BEF+∠DFE=

260

260

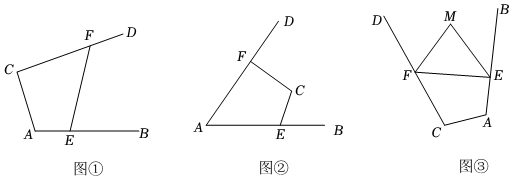
度．
【探究】如图②，在四边形AECF中，EB、FD分别是边AE、AF的延长线，我们把∠BEC、∠DFC称为四边形AECF的外角，试探究∠A、∠C与∠BEC、∠DFC之间的数量关系，并说明理由．
【应用】如图③，FM、EM分别是四边形AEFC的外角∠DFE、∠BEF的平分线，若∠A+∠C=210°，则∠M的度数为

75°

75°

．