如图1是某条公路的一个具有两条车道的隧道的横断面．经测量，两侧墙AD和BC与路面AB垂直，隧道内侧宽AB=8米．为了确保隧道的安全通行，工程人员在路面AB上取点E，测量点E到墙面AD的距离AE，点E到隧道顶面的距离EF．设AE=x米，EF=y米．通过取点、测量，工程人员得到了x与y的几组值，如表：
| x（米） | 0 | 2 | 4 | 6 | 8 |
| y（米） | 4.0 | 5.5 | 6.0 | 5.5 | 4.0 |
（1）根据上述数据，直接写出隧道顶面到路面AB的最大距离为
6.0
6.0
米，并求出满足的函数关系式y=a（x-h）2+k（a＜0）；（2）请你帮助工程人员建立平面直角坐标系，描出表中各对对应值为坐标的点，画出可以表示隧道顶面的函数的图象（图2）．
（3）若如图3的汽车在隧道内正常通过时，汽车的任何部位需到左侧墙及右侧墙的距离不小于1米且到隧道顶面的距离不小于0.35米．按照这个要求，隧道需标注的限高应为多少米（精确到0.1米）？
【考点】二次函数的应用．
【答案】6.0
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：497引用：7难度：0.5
相似题
-
1．某服装店销售某种衣服，其成本为每件60元，当售价为每件100元时，每月可销售120件．由于疫情的影响，库存积压严重，为了减少库存，该服装店采取降价措施．据市场调查反映：销售单价每降5元，则每月可多销售20件．设每件的售价为x元（x为正整数），每月的销售量为y件．
（1）直接写出y与x的函数关系式；
（2）当销售单件降低多少元时，每月获得的利润最大，最大利润是多少？发布：2025/5/23 1:30:2组卷：27引用：1难度：0.5 -
2．某产品每件成本是10元，试销阶段每件产品的售价x（元）与日销售量y（件）之间的关系如下表：
已知日销售量y是售价x的一次函数．x（元） 15 20 30 … y（件） 25 20 10 …
（1）求y与x的函数表达式；
（2）当销售价为多少时，每日的销售利润最大？最大利润是多少？发布：2025/5/23 2:0:6组卷：157引用：3难度：0.6 -
3．某园艺公司计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1（万元）与投入资金x（万元）成正比例关系，如图1所示；种植花卉的利润y2（万元）与投入资金x（万元）成二次函数关系，如图2所示．
（1）分别求出利润y1（万元）与y2（万元）关于投入资金x（万元）的函数关系式；
（2）如果该园艺公司以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？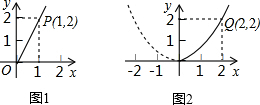
发布：2025/5/23 1:30:2组卷：149引用：5难度：0.7
