在一次数学活动课上，老师要求同学们画15°、30°和60°角，小强同学身旁没有量角器，也没有圆规、三角尺，他灵机一动，想到了折纸的办法：他拿出一张矩形纸片ABCD，先对折使AD与BC重合，如图一，得到折痕EF，把纸片展开，再一次折叠纸片ABCD，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM和线段BN．
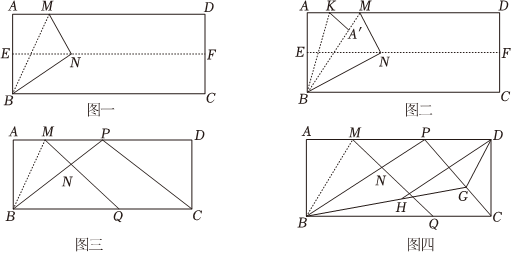
（1）请直接写出∠ABM的度数，并说明理由；
（2）在图一的线段AM上取一点K，将△ABK沿着直线BK折叠，如图二，使得A点恰好落在线段BM上，求tan∠ABK；
（3）若M为AD边上的一点，如图三，将△ABM沿直线BM折叠，A的对应点为N，延长MN交BC边于点Q，延长BN交AD边于点P，连接CP．
①若ADAB=n，当AB=2cm时，若存在唯一的点P，使得四边形MQCP为平行四边形，求n的值；
②在①的条件下，若G为线段CP上一动点，如图四，连接BG，取线段BG的中点H，连接DH，求DH的最小值．
AD
AB
=
n
【考点】解三角形．
【答案】（1）∠ABM=30°；（2）；（3）①n=2；②．
tan
∠
ABK
=
2
-
3
DH
=
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/29 8:0:9组卷：135引用：4难度：0.1
相似题
-
1．在①
，②2a-c=2bcosC，③（a-b）（a+b）=（a-c）c这三个条件中任选一个，补充在下面的问题中，并解答该问题．3（a-bcosC）=csinB
在△ABC中，内角A，B，C的对边分别是a,b,c,且满足 _____，．b=23
（1）若a+c=4，求△ABC的面积；
（2）求△ABC周长l的取值范围．发布：2024/12/29 13:0:1组卷：287引用：4难度：0.5 -
2．已知灯塔A在海洋观察站C的北偏东65°，距离海洋观察站C的距离为akm,灯塔B在海洋观察站C的南偏东55°，距离海洋观察站C的距离为3akm,则灯塔A与灯塔B的距离为（ ）
发布：2024/12/30 4:0:3组卷：50引用：3难度：0.7 -
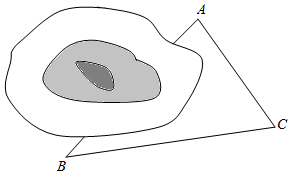3．如图，在铁路建设中，需要确定隧道两端的距离（单位：百米），已测得隧道两端点A，B到某一点C的距离分别为5和8，∠ACB=60°，则A，B之间的距离为（ ）发布：2024/12/29 13:0:1组卷：295引用：5难度：0.7
