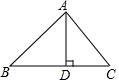
通过学习锐角三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=底边腰=BCAB,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
(1)can30°=33;
(2)如图(2),已知在△ABC中,AB=AC,canB=85,S△ABC=24,求△ABC的周长.

底边
腰
=
BC
AB
3
3
8
5
【答案】
3
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/12 11:0:13组卷:587引用:6难度:0.5