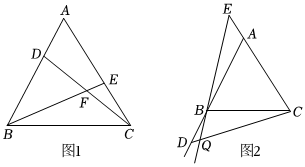
如图1，△ABC中，AB=BC=CA，∠A=∠ABC=∠ACB=60°，在△ABC的顶点A，C处各有一只小蚂蚁，它们同时出发，分别以相同速度由A向B和由C向A爬行，经过t（s）后，它们分别爬行到了D，E处，连接DC，BE，DC与BE相交于点F．
（1）求证：△ACD≌△CBE；
（2）小蚂蚁在爬行过程中，∠BFC的大小会变化吗？若变化，请说明理由；若不变，求∠BFC的度数；
（3）如图2，当小蚂蚁分别爬行到线段AB，CA的延长线上的D，E处时，若EB的延长线与CD交于点Q，其他条件不变，请直接写出∠CQE的度数．
【考点】三角形综合题．
【答案】（1）证明见解答过程；
（2）∠BFC无变化．其度数为120°；
（3）60°．
（2）∠BFC无变化．其度数为120°；
（3）60°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/19 18:0:1组卷：104引用：5难度：0.2
相似题
-
1．已知动点P以每秒1cm的速度沿图（1）的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的△ABP的面积S与时间t之间的关系如图（2）中的图象表示．若AB=3cm,试回答下列问题
（1）图（1）中的BC长是多少？
（2）图（2）中的a是多少？
（3）图（1）中的图形面积是多少？
（4）图（2）中的b是多少？发布：2025/6/15 5:30:3组卷：343引用：2难度：0.3 -
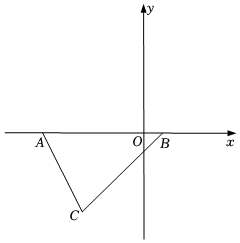2．如图，在平面直角坐标系中，A（a,0），B（b,0），且满足，C在第三象限，坐标为（n+1，n），连接AC，BC，（a+5）2+b-1=0
（1）请直接写出：a=，b=，AB=，S△ABC=（用含n的代数式表示）；
（2）在线段AB上取一点D，连接CD并延长，交y轴于点E，连接AE，BE，
①若S△DCA=2S△DEA，求点E坐标，用含n的代数式表示．
②若S△ADC=S△DBE，求点E坐标．发布：2025/6/15 14:0:2组卷：144引用：1难度：0.1 -
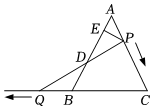3．如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A，C不重合），Q是CB延长线上一点，由B向CB延长线方向运动（Q不与B重合），连接PQ交AB于D，过P作PE⊥AB于E．若两点同时出发，以相同的速度每秒1个单位运动，运动时间为t.
（1）当∠PQC=30°时，求t的值；
（2）求证：PD=DQ；
（3）当P，Q在运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．发布：2025/6/15 6:30:1组卷：151引用：1难度：0.4
