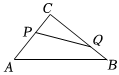
如图，在Rt△ABC中，∠C=90°，AC=3厘米，CB=4厘米．两个动点P，Q分别从A，C两点同时按顺时针方向沿△ABC的边运动．当点Q运动到点A时，P，Q两点运动即停止．点P，Q的运动速度分别为1厘米/秒、2厘米/秒，设点P运动的时间为t（秒）．记线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形的面积为S（平方厘米）．
（1）用含t的代数式表示PC的长；
（2）当点P，Q运动时，求S与时间t的函数关系式，并写出自变量t的取值范围；
（3）点P，Q在运动的过程中，S有最大值吗？若有，请求出最大值；若没有，请说明理由．
【考点】三角形综合题．
【答案】（1）当点P在AC边上运动时，PC=3-t；当点P在CB边上运动时，PC=t-3．
（2）
，
（3）当 时，S有最大值为 ．
（2）
S
=
- t 2 + 3 t （ 0 ＜ t ≤ 2 ） |
4 5 t 2 - 18 5 t + 6 （ 2 ＜ t ≤ 3 ） |
- 3 5 t 2 + 27 5 t - 42 5 （ 3 ＜ t ≤ 9 2 ） |
（3）当
t
=
9
2
15
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/3 8:0:9组卷：27引用：1难度：0.5
相似题
-
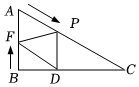1．如图，在Rt△ABC中，∠ABC=90°，∠C=30°，AB=9cm，动点P从点A开始以2cm/s的速度向点C运动，动点F从点B开始以1cm/s的速度向点A运动，两点同时运动，同时停止，运动时间为t（s）．
（1）当t为何值时，△PAF是等边三角形？
（2）当t为何值时，△PAF是直角三角形？
（3）过点P作PD⊥BC于点D，连接DF．
①求证：四边形AFDP是平行四边形；
②当t为何值时，△PDC的面积是△ABC面积的一半．发布：2025/5/24 1:0:1组卷：283引用：3难度：0.3 -
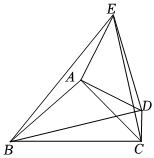2．如图，在△ABC中，AB=AC=3，∠BAC=90°，点D为一个动点，且点D到点C的距离为1，连接CD，AD，作EA⊥AD，使AE=AD．
（1）求证：△ADB≌△AEC；
（2）求证：BD⊥EC；
（3）直接写出BD最大和最小值；
（4）点D在直线AC上时，求BD的长．发布：2025/5/23 21:0:1组卷：103引用：2难度：0.4 -
3．在一次数学兴趣小组活动中，小明将两个形状相同，大小不同的三角板AOB和三角板DEB放置在平面直角坐标系中，点O（0，0），A（0，3），∠ABO=30°，BE=3．
（Ⅰ）如图①，求点D的坐标；
（Ⅱ）如图②，小明同学将三角板DEB绕点B按顺时针方向旋转一周．
①若点O，E，D在同一条直线上，求点D到x轴的距离；
②连接DO，取DO的中点G，在旋转过程中，点G到直线AB的距离的最大值是 （直接写出结果即可）．发布：2025/5/24 1:0:1组卷：573引用：2难度：0.3
