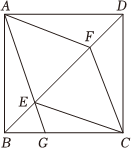
如图，正方形ABCD中，AB=2，点E，F是对角线BD上的两点，且BE=DF．（1）求证：△ABE≌△ADF；
（2）试判断四边形AECF的形状，并加以证明．
（3）设AE的延长线交BC边于点G，若点G恰为BC边的中点，求四边形AECF的周长与面积．
【考点】正方形的性质；全等三角形的判定与性质．
【答案】（1）证明见解答过程；
（2）四边形AECF是菱形．证明见解答过程；
（3）；．
（2）四边形AECF是菱形．证明见解答过程；
（3）
8
5
3
4
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/1 8:0:9组卷：82引用：1难度：0.5
相似题
-
1．如图，正方形ABCD边长为2，E为CD的中点，以点A为中心，把△ADE顺时针旋转90°得△ABF，连接EF，则EF的长等于．发布：2025/6/20 8:30:2组卷：246引用：16难度：0.9 -
2．在正方形ABCD中，P为AB的中点，BE⊥DP的延长线于点E，连接AE，FA⊥AE交DP于点F，连接BF、FC．下列结论：①△ABE≌△ADF；②FB=AB；③CF⊥DP；④FC=EF．其中正确的结论为 ．（请将所有正确的序号都填上）发布：2025/6/20 9:30:2组卷：186引用：2难度：0.5 -
3．我们知道，面动成体！如图，正方形ABCD边长为3cm,以直线AB为轴将正方形旋转一周所得几何体，从正面看到的形状图的面积是（ ）发布：2025/6/20 7:30:1组卷：48引用：3难度：0.7
