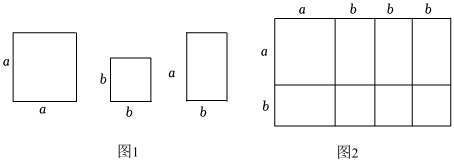
【阅读理解】在苏科版七下教材第九章的学习中，我们了解了因式分解，除了提取公因式、运用公式法外，还有其他方法可帮助我们快速对一个多项式进行因式分解．以a²+4ab+3b²为例，小明参考教材P88数学活动“拼图•公式”，拼出了如图2的长方形；

小红则参考课外阅读，认识了“配方法”，给到如下过程：
a²+4ab+3b²
=a²+4ab+（2b）²-（2b）²+3b²，
=（a+2b）²-（2b）²+3b²，
=（a+2b）²-4b²+3b²，
=…
【尝试解决】
（1）由拼图可得等式a²+4ab+3b²=

（a+3b）（a+b）

（a+3b）（a+b）

；
（2）请接着小红的思路补全解答过程；
（3）上述两种方法，任选一种将a²+5ab+6b²因式分解．（注：若选择拼图法，请画出图形，并做适当标注；若选配方法，请写完整过程）
【实际应用】
（4）学校有一长方形空地，为了美化校园环境，现欲规划1块a×a型、6块b×b型正方形和5块a×b型小长方形区域（a、b都是正整数），种植不同种类的花草．若长方形空地总面积为35m²，求出a、b的值分别是多少？