如图,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,当点D在线段BC上时(与点B不重合),如图1,线段CF、BD所在直线的位置关系为 CF⊥BDCF⊥BD;线段CF、BD的数量关系为 CF=BDCF=BD;
(2)当点D在线段BC的延长线上时,如图2,(1)中的结论是否仍然成立,并说明理由;
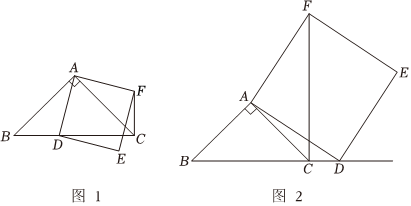
(3)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
【考点】四边形综合题.
【答案】CF⊥BD;CF=BD
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/23 6:0:3组卷:36引用:1难度:0.1
相似题
-
1.已知:四边形ABCD,连接AC,AD=CD,∠DAC=∠ABC,∠DCA=∠BAC,AD∥BC.
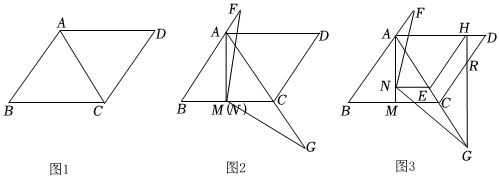
(1)如图1,求证:△ABC是等边三角形;
(2)过点A作AM⊥BC于点M,点N为AM上一点(不与点A重合),∠FNG=120°,∠FNG的边NF交BA的延长线于点F,另一边NG交AC的延长线于点G,如图2,点N与点M重合时,求证:NF=NG;
(3)如图3,在(2)的条件下,点N不与点M重合,过点N作NE⊥AM,交AC于点E,EN:CM=3:4,AF=3,CG=4,点H为AD上一点,连接EH、GH,GH交CD于点R,EH=EG,求DR的长.发布:2025/5/29 15:30:1组卷:155引用:1难度:0.1 -
2.综合与实践:在数学课上,王老师让同学们对两个全等的直角三角形纸片进行摆弄,如图1,Rt△ABC≌Rt△DEF,∠ACB=∠DFE=90°.

(1)如图2,将图1的两个直角三角形的斜边AB、DE重合,得到“筝形ACBF”,连接CF交AB于点O,若AF=2BC,则S△CBO:S△AFO=;
(2)如图3,将图1的两个直角三角形直角顶点C与顶点F重合,AB∥DE,连接BE,AD,求证:四边形ADEB是矩形;
(3)如图4,将图1的两个直角三角形的边AB、DE放到同一直线上,点C、F在AB的同侧,连接CE,AF,CF,若点E是AB的中点.请判断四边形CEAF的形状,并说明理由.发布:2025/5/29 15:30:1组卷:47引用:2难度:0.3 -
3.已知:如图1,在平面直角坐标系中,点A、点B分别在x轴、y轴的正半轴上,点C在第一象限,∠ACB=90°,AC=BC,点A坐标为(m,0),点C横坐标为n,且(m-1)2+n2-8n+16=0.
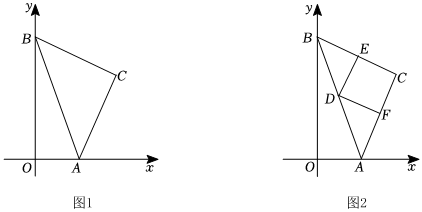
(1)分别求出点A、点B、点C的坐标;
(2)如图2,点D为边AB中点,以点D为顶点的直角∠EDF两边分别交边BC于E,交边AC于F,①求证:DE=DF;②求证:S四边形DECF=S△ABC;12
(3)在坐标平面内有点G(点G不与点A重合),使得△BCG是等腰直角三角形,请直接写出满足条件的点G的坐标.发布:2025/5/29 16:0:1组卷:121引用:1难度:0.1


