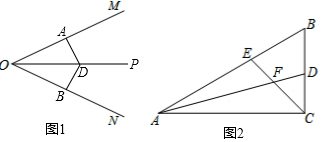
观察发现：
如图1，OP平分∠MON，在OM，ON上分别取OA，OB，使OA=OB，再在OP上任取一点D，连接AD，BD．请你猜想AD与BD之间的数量关系，并说明理由．
拓展应用：
如图2，在△ABC中，∠ACB是直角，∠B=60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F，请你写出FE与FD之间的数量关系，并说明理由．
【考点】全等三角形的判定与性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：1429引用：4难度：0.5
相似题
-
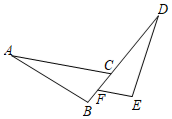1．如图，AC∥EF，点F、C在BD上，AC=DF，BC=EF，求证：∠A=∠D．发布：2025/6/22 19:30:1组卷：24引用：2难度：0.7 -
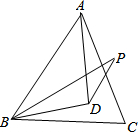2．如图，D是等边△ABC内一点，DB=DA，BP=AB，∠DBP=∠DBC，求证：∠P=30°．发布：2025/6/22 20:0:1组卷：253引用：3难度：0.1 -
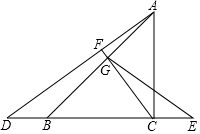3．如图，已知△ABC为等腰直角三角形，∠C=90°，D、E为直线BC上两点且满足BD=CE，连接AD，过点C作CF⊥AD交AB于点G，垂足为F，连接EG，
（1）若AC=6，CE=2，求CF的长；
（2）求证：EG+CG=AD．发布：2025/6/22 20:30:1组卷：216引用：2难度：0.1
