任意球是足球比赛的主要得分手段之一，在某次足球比赛中，李强站在点O处发出任意球，如图，把球看作点，其运行轨迹的高度y（m）与水平距离x（m）满足函数关系式y=a（x-12）2+h,李强罚任意球时防守队员站在李强前方8米处组成人墙，防守队员的身高为2米，对手球门与李强的水平距离为18米，已知足球球门的宽是7.32米，高是2.43米．
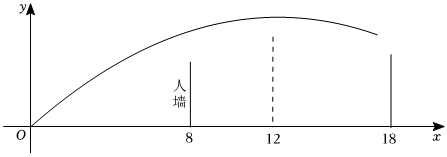
（1）当h=3时，求y与x的函数关系式；
（2）在第（1）问的前提下，足球能否越过人墙？足球能否直接射进球门？请说明理由；
（3）若李强罚出任意球一定能直接射进球门得分，直接写出h的取值范围．
【考点】二次函数的应用．
【答案】（1）；
（2）足球能越过人墙，能直接射进球门，理由见解析；
（3）2.25＜h＜3.24．
y
=
-
1
48
（
x
-
12
）
2
+
3
（2）足球能越过人墙，能直接射进球门，理由见解析；
（3）2.25＜h＜3.24．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：431引用：3难度：0.5
相似题
-
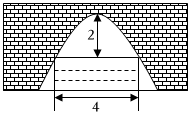1．如图所示为一座纵截面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m,当水位下降1m时，水面的宽度为（ ）发布：2025/6/8 9:0:1组卷：105引用：1难度：0.6 -
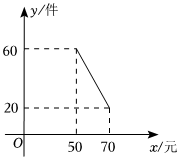2．某商店试销一种新商品，新商品的进价为30元/件，经过一段时间的试销发现，每月的销售量会因售价的调整而不同．令每月销售量为y件，售价为x元/件，每月的总利润为Q元．
（1）当售价在40≤x≤50元时，每月销售量都为60件，则此时每月的总利润最多是多少元？
（2）当售价在50≤x≤70元时，每月销售量与售价的关系如图所示，则此时当该商品售价x是多少元时，该商店每月获利最大，最大利润是多少元？发布：2025/6/8 9:0:1组卷：56引用：3难度：0.6 -
3．为了巩固脱贫攻坚成效，助推乡村振兴，最近市委市政府又出台了系列“惠农”政策，农民收入大幅增加．某村一农户生产经销一种农副产品，已知这种产品的成本为5元/千克，售价为6元/千克时，当天的销售量为100千克．在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5千克．设当天销售单价统一为x元/千克（x≥6，且x是按0.5元的整数倍上涨），当天的销售利润为y元．
（1）求y与x之间的函数关系式，不要求写出自变量x的取值范围；
（2）若物价部门核定该产品的利润率不得超过80%，该产品的售价定为多少元时，才能使当天获得最大利润？最大利润是多少？发布：2025/6/8 8:0:6组卷：38引用：1难度：0.6
