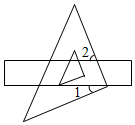
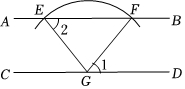
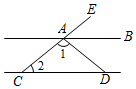
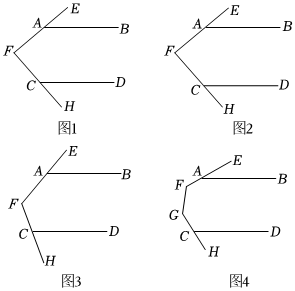
如图1，已知∠EFH=90°，点A，C分别在射线FE和FH上，在∠EFH内部作射线AB，CD，使AB平行于CD．
（1）如图1，若∠FAB=150°，求∠HCD的度数；
（2）小颖发现，在∠EFH内部，无论∠FAB如何变化，∠FAB-∠HCD的值始终为定值，请你结合图2求出这一定值；
（3）①如图3，把图1中的∠EFH=90°改为∠EFH=120°，其他条件不变，请直接写出∠FAB与∠HCD之间的数量关系；
②如图4，已知∠EFG+∠FGC=α，点A，C分别在射线FE，GH上，在∠EFG与∠FGH内部作射线AB，CD，使AB平行于CD，请直接写出∠FAB与∠HCD之间的数量关系．
【考点】平行线的性质．
【答案】（1）60°；
（2）90°；
（3）①∠FAB-∠HCD=60°；②∠FAB-∠HCD=360°-α．
（2）90°；
（3）①∠FAB-∠HCD=60°；②∠FAB-∠HCD=360°-α．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/15 8:0:9组卷：20引用：2难度：0.5
